题目内容
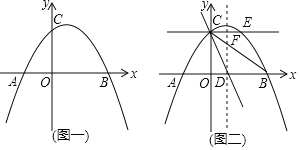
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A. B两点,与y轴交于点D(0,6).
+bx+c经过A. B两点,与y轴交于点D(0,6).
(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由。
【答案】(1)![]() ;(2)DE=
;(2)DE=![]() +6=
+6=![]() ;(3)S=
;(3)S=![]() (2<m<4);(4)N点坐标为(
(2<m<4);(4)N点坐标为(![]() );(
);( ![]() )
)
【解析】
(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为![]()
(2)先利用待定系数法求得直线AC的解析式为y=![]() ,则可确定E(0,
,则可确定E(0,![]() ),然后计算DE的长;
),然后计算DE的长;
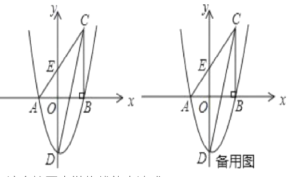
(3)如图1,作PQ∥y轴交AC于Q,设P(m,![]() -6),则Q(m,
-6),则Q(m,![]() ),则PQ=-
),则PQ=-![]() ,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组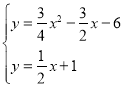 得N点坐标为(
得N点坐标为(![]() );当点M′在x的负半轴上时,AN′交y轴与G,先在证明Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组
);当点M′在x的负半轴上时,AN′交y轴与G,先在证明Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组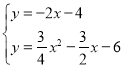 得N的坐标.
得N的坐标.
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),C(0,6)代入y=![]() +bx+c得
+bx+c得![]() ,解得
,解得 ,
,
∴抛物线解析式为![]() ;
;
(2)设直线AC的解析式为y=px+q,
把A(2,0),C(4,8)代入得![]() ,解得
,解得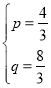 ,
,
∴直线AC的解析式为y=![]() ,
,
当x=0时,y=![]() =
=![]() ,则E(0,
,则E(0, ![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
(3)如图1,作PQ∥y轴交AC于Q,
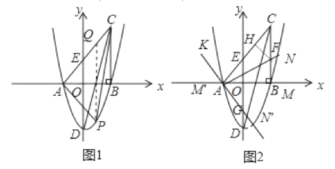
设P(m,![]() -6),则Q(m,
-6),则Q(m,![]() ),
),
∴PQ=-![]() ,
,
∴S=S△PAQ+S△PCQ=![]() 6PQ=
6PQ=![]() (2<m<4);
(2<m<4);
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,则FH=FB,
易得AH=AB=6,
∵AC=![]() =
=![]() =10,
=10,
∴CH=106=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() =5,
=5,
∴F(4,3),
易得直线AF的解析式为y=![]() x+1,
x+1,
解方程组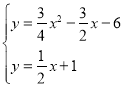 得
得![]() 或
或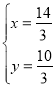 ,
,
∴N点坐标为(![]() );
);
当点M′在x的负半轴上时,AN′交y轴与G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,4),
易得直线AG的解析式为y=2x4,
解方程组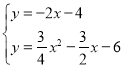 得
得![]() 或
或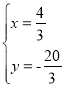 ,
,
∴N′的坐标为(![]() ),
),
综上所述,满足条件的N点坐标为(![]() );(
);( ![]() )
)

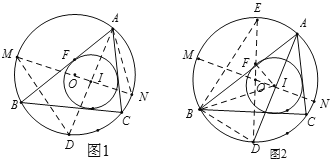
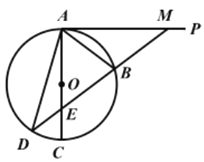
【题目】如图,AC是⊙O的一条弦,AP是⊙O的切线。作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
【题目】一辆汽车油箱中有汽油![]() .如果不再加油,那么油箱中的油量
.如果不再加油,那么油箱中的油量![]() (单位:
(单位:![]() )随行驶路程
)随行驶路程![]() (单位:
(单位:![]() )的增加而减少.已知该汽车平均耗油量为
)的增加而减少.已知该汽车平均耗油量为![]() .
.
(Ⅰ)计算并填写下表:
| 10 | 100 | 300 | … |
| … |
(Ⅱ)写出表示![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,
,![]() 两地的路程约有
两地的路程约有![]() ,当油箱中油量少于
,当油箱中油量少于![]() 时,汽车会自动报警,则这辆汽车在由
时,汽车会自动报警,则这辆汽车在由![]() 地到
地到![]() 地,再由
地,再由![]() 地返回
地返回![]() 地的往返途中,汽车是否会报警?请说明理由.
地的往返途中,汽车是否会报警?请说明理由.