题目内容
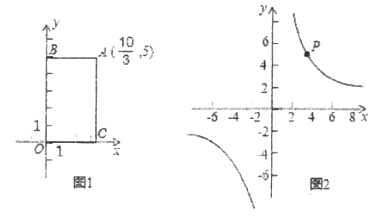
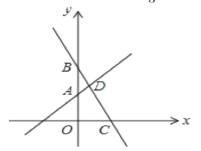
【题目】如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(![]() ,n)
,n)
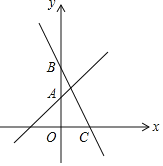
(1)则n= ,k= ,b=_______.
(2)若函数y=kx+b的函数值大于函数y=x+2的函数值,则x的取值范围是_______.
(3)求四边形AOCD的面积.
【答案】(1)![]() ,2,4;(2)x<
,2,4;(2)x<![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据点D在函数y=x+2的图象上,即可求出n的值;再利用待定系数法求出k,b的值;
(2)根据图象,直接判断即可;
(3)用三角形OBC的面积减去三角形ABD的面积即可.
(1)∵点D(![]() ,n)在直线y=x+2上,
,n)在直线y=x+2上,
∴n=![]() +2=
+2=![]() ,
,
∵一次函数经过点B(0,4)、点D(![]() ,
, ![]() ),
),
∴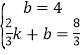 ,解得:
,解得:![]() ,
,
故答案为:![]() ,2,4;
,2,4;
(2)由图象可知,函数y=kx+b大于函数y=x+2时,图象在直线x=![]() 的左侧,
的左侧,
∴x<![]() ,
,
故答案为:x<![]() ,
,
(3)直线y=2x+4与x轴交于点C,
∴令y=0,得:2x+4=0,解得x=2,
∴点C的坐标为(2,0),
∵函数y=x+2的图象与y轴交于点A,
∴令x=0,得:y=2,
∴点A的坐标为(0,2),
S![]() =
=![]() ×2×4=4,
×2×4=4,
S![]() =
=![]() ×(42)×
×(42)×![]() =
=![]() ,
,
∴S![]() =S
=S![]() S
S![]() =4
=4![]() =
=![]() .
.

练习册系列答案
相关题目