题目内容
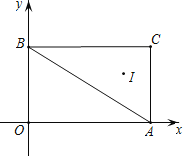
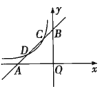
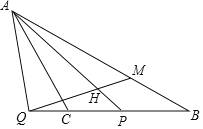
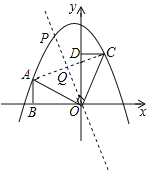
【题目】如图,Rt△ABO的直角边OB在x轴上,OB=2,AB=1,将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO,抛物线y=﹣![]() +bx+c经过A,C两点.
+bx+c经过A,C两点.
(1)求点A,C的坐标;
(2)求二次函数的解析式;
(3)连接AC,点P是抛物线上一点,直线OP把△AOC的周长分成相等的两部分,求点P的坐标.

【答案】(1)A(﹣2,1),C(1,2);(2)y=-![]() -
-![]() x+
x+![]() ;(3)(4,﹣12)或(﹣1,3)
;(3)(4,﹣12)或(﹣1,3)
【解析】
(1)根据线段OB、AB的长度易得点A的坐标,根据旋转的性质求得C点的坐标;
(2)根据待定系数法即可求得;
(3)由直线OP把△AOC的周长分成相等的两部分且OA=OC,知AQ=CQ,即点Q为AC的中点,从而得出点Q坐标,求得直线OP解析式,联立方程可得点P坐标.
解:(1)∵OB=2,AB=1,
∴A(﹣2,1),
将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO,
∴C(1,2),
(2)∵抛物线y=﹣![]() +bx+c经过A,C两点,
+bx+c经过A,C两点,
∴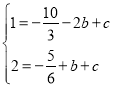 ,解得
,解得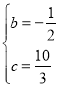
∴二次函数的解析式为y=﹣![]() ﹣
﹣![]() x+
x+![]() ;
;
(3)设OP与AC交于点Q,
∵OP将△AOC的周长分成相等的两部分,又OA=OC,OQ=OQ,
∴AQ=CQ,即Q为AC的中点,
∴Q(﹣![]() ,
,![]() ).
).
设直线OP的解析式为y=kx,把Q(﹣![]() ,
,![]() )代入y=kx,得
)代入y=kx,得![]() =﹣
=﹣![]() k,
k,
∴k=﹣3.
∴直线OP的解析式为y=﹣3x.
由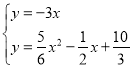 ,得
,得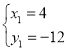 ,
,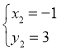 ,
,
∴P1(4,﹣12),P2(﹣1,3).

练习册系列答案
相关题目