题目内容
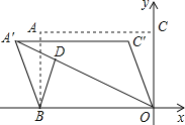
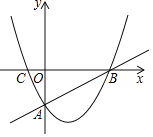
【题目】如图,直线y=![]() x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣
x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣![]() x+c经过A,B两点,与x轴的另一交点为C.
x+c经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)M为抛物线上一点,直线AM与x轴交于点N,当![]() 时,求点M的坐标;
时,求点M的坐标;
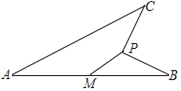
(3)P为抛物线上的动点,连接AP,当∠PAB与△AOB的一个内角相等时,直接写出点P的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)点P的坐标为:(﹣1,0)或(
x﹣2;(2)点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)点P的坐标为:(﹣1,0)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() )或(3,﹣2).
)或(3,﹣2).
【解析】
(1)根据题意直线y=![]() x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,-2)、(4,0),即可求解;
x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,-2)、(4,0),即可求解;
(2)由题意直线MA的表达式为:y=(![]() m﹣
m﹣![]() )x﹣2,则点N(
)x﹣2,则点N(![]() ,0),当
,0),当![]() =
=![]() 时,则
时,则![]() =
=![]() ,即
,即 =
=![]() ,进行分析即可求解;
,进行分析即可求解;
(3)根据题意分∠PAB=∠AOB=90°、∠PAB=∠OAB、∠PAB=∠OBA三种情况,分别求解即可.
解:(1)直线y=![]() x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,﹣2)、(4,0),
x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,﹣2)、(4,0),
则c=﹣2,将点B的坐标代入抛物线表达式并解得:a=![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣2①;
x﹣2①;
(2)设点M(m,![]() m2﹣
m2﹣![]() m﹣2)、点A(0,﹣2),
m﹣2)、点A(0,﹣2),

将点M、A的坐标代入一次函数表达式:y=kx+b并解得:
直线MA的表达式为:y=(![]() m﹣
m﹣![]() )x﹣2,
)x﹣2,
则点N(![]() ,0),
,0),
当![]() =
=![]() 时,则
时,则![]() =
=![]() ,即:
,即: =
=![]() ,
,
解得:m=5或﹣2或2或1,
故点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);
(3)①∠PAB=∠AOB=90°时,
则直线AP的表达式为:y=﹣2x﹣2②,
联立①②并解得:x=﹣1或0(舍去0),
故点P(﹣1,0);
②当∠PAB=∠OAB时,
当点P在AB上方时,无解;
当点P在AB下方时,

将△OAB沿AB折叠得到△O′AB,直线OA交x轴于点H、交抛物线为点P,点P为所求,
则BO=OB=4,OA=OA=2,设OH=x,
则sin∠H=![]() ,即:
,即:![]() ,解得:x=
,解得:x=![]() ,则点H(﹣
,则点H(﹣![]() ,0),.
,0),.
则直线AH的表达式为:y=﹣![]() x﹣2③,
x﹣2③,
联立①③并解得:x=![]() ,故点P(
,故点P(![]() ,﹣
,﹣![]() );
);
③当∠PAB=∠OBA时,
当点P在AB上方时,

则AH=BH,
设OH=a,则AH=BH=4﹣a,AO=2,
故(4﹣a)2=a2+4,解得:a=![]() ,
,
故点H(![]() ,0),
,0),
则直线AH的表达式为:y=![]() x﹣2④,
x﹣2④,
联立①④并解得:x=0或![]() (舍去0),
(舍去0),
故点P(![]() ,
,![]() );
);
当点P在AB下方时,
同理可得:点P(3,﹣2);
综上,点P的坐标为:(﹣1,0)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() )或(3,﹣2).
)或(3,﹣2).