题目内容
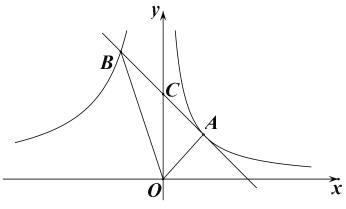
【题目】如图,抛物线y=﹣![]() x2+bx+c,经过矩形OABC的A(3,0),C(0,2),连结OB.D为横轴上一个动点,连结CD,以CD为直径作⊙M,与线段OB有一个异于点O的公共点E,连结DE.过D作DF⊥DE,交⊙M于F.
x2+bx+c,经过矩形OABC的A(3,0),C(0,2),连结OB.D为横轴上一个动点,连结CD,以CD为直径作⊙M,与线段OB有一个异于点O的公共点E,连结DE.过D作DF⊥DE,交⊙M于F.
(1)求抛物线的解析式;
(2)tan∠FDC的值;
(3)①当点D在移动过程中恰使F点落在抛物线上,求此时点D的坐标;
②连结BF,求点D在线段OA上移动时,BF扫过的面积.

【答案】(1) y=﹣![]() x2+
x2+![]() x+2;(2)
x+2;(2)![]() ;(3)①(﹣
;(3)①(﹣![]() ,0);②3
,0);②3
【解析】
(1)将点A、C的坐标代入抛物线的表达式,即可求解;
(2) 连接CE、CF、FO,证明∠FDC=∠ECD=∠EOD=∠BOA,即可求解;
(3) ①如图2,连接FO,则∠FOG=∠FCD,证明∠FOG=∠FCD=∠CDE=∠COE,通过tan∠FOG=tan∠COB=![]() ,来确定直线OF的表达式,进而求解;
,来确定直线OF的表达式,进而求解;
②如图3,当点D、O重合时,连接CF、BF,由①知tan∠FOG=![]() ,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,由①同理可得:△CHF∽△FGO,则
,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,由①同理可得:△CHF∽△FGO,则![]() ,求得a的值,根据BF扫过的面积为△BOF的面积,即可求解.
,求得a的值,根据BF扫过的面积为△BOF的面积,即可求解.
解:(1)将点A、C的坐标代入抛物线的表达式得: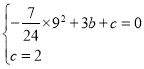 ,
,
解得: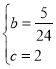 ,
,
故抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图1,连接CE、CF、FO,
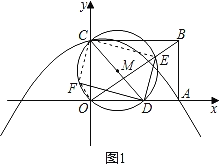
∵CD是直径,
∴∠CED=90°,即CE⊥DE,
又∵DF⊥DE,
∴∠FDC=∠ECD=∠EOD=∠BOA,
∴tan∠FDC=tan∠BOA=![]() ;
;
(3)①如图2,
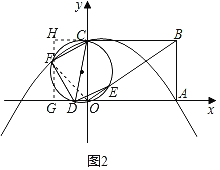
连接FO,则∠FOG=∠FCD,
∵CD是直径,
∴∠CFD=90°,
同理∠FDE=90°,
∴FC∥DE,
∴∠FCD=∠CDE=∠COE,
∴∠FOG=∠FCD=∠CDE=∠COE,
∴tan∠FOG=tan∠COE=tan∠COB=![]() ,
,
故直线OF的表达式为:y=﹣![]() x②,
x②,
联立①②并解得: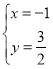 ,故点F(﹣1,
,故点F(﹣1,![]() );
);
过点F作y轴的平行线GH,交x轴于点G,交过点C与x轴的平行线于点H,
∴FG=![]() ,CH=1,HF=2﹣
,CH=1,HF=2﹣![]() =
=![]() ,
,
∵∠HFC+∠GFD=90°,∠HFC+∠HCF=90°,
∴∠HCF=∠GFD,
又∠CHF=∠FGD=90°,
∴△CHF∽△FGD,
∴![]() ,即
,即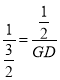 ,解得:GD=
,解得:GD=![]() ,
,
∴OD=1﹣![]() =
=![]() ,
,
故点D的坐标为:(﹣![]() ,0);
,0);
②如图3,当点D、O重合时,连接CF、BF,

则BF扫过的面积为△BOF的面积,∠CFO=90°,
过点F作y轴的平行线HG,交x轴于点G,交过点C与x轴的平行线于点H,
由①同理可得:△CHF∽△FGO,则![]() ,
,
由①知tan∠FOG=![]() ,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,
,设FG=3a,则OG=2a=HC,HF=2﹣GF=2﹣3a,
∴![]() ,解得:a=
,解得:a=![]() ;
;
在Rt△FOG中,FO=![]() ,
,
同理在Rt△AOB中,OB=![]() ,
,
∵EF是圆的直径,故OF⊥OE,
BF扫过的面积=S△BOF=![]() ×BO×FO=
×BO×FO=![]() ,
,
故BF扫过的面积为3.

 阅读快车系列答案
阅读快车系列答案【题目】某公司计划投资![]() 万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为
万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为![]() 件,每件总成本为
件,每件总成本为![]() 万元,每件出厂价
万元,每件出厂价![]() 万元;流水生产线投产后,从第
万元;流水生产线投产后,从第![]() 年到第
年到第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)如下表:
(万元)如下表:
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)与
(万元)与![]() 的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)投产第几年该公司可收回![]() 万元的投资?
万元的投资?
(3)投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?