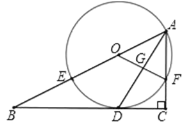
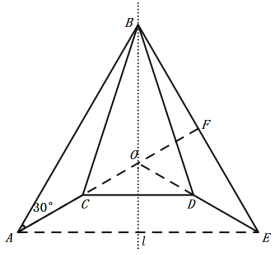
题目内容
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 关于直线
关于直线![]() 的轴对称图形
的轴对称图形![]() 点
点![]() 是
是![]() 的中点,若点
的中点,若点![]() 在同一直线上,则
在同一直线上,则![]() 的长为___________.
的长为___________.
【答案】3
【解析】
先证得△ABF为直角三角形,继而证得△ABE为等边三角形,利用三角形重心的性质结合三角形中位线定理即可求解.
如图,连接CF,过B作BG⊥AF于G,
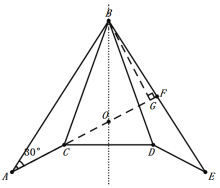
∵点A、C、F在同一直线上,
∴∠BAF=∠A=30![]() ,
,
在Rt△ABG中,∠A=30![]() ,AB=6,
,AB=6,
∴BG=3,
根据对称的性质,BE=AB=6,
∵点F是BE的中点,
∴BF=![]() BE=3,
BE=3,
∴点F、G重合,
∴∠AFB=90![]() ,;
,;
如图,连接AE,连接CF交直线![]() 于点O,连接OD,
于点O,连接OD,
∵∠AFB=90![]() ,∠BAF =30
,∠BAF =30![]() ,
,
∴∠ABE=60![]() ,
,
∵BE=AB=6,
∴△ABE是等边三角形,
∴O是△ABE的重心,
∴AF=![]() BF=3
BF=3![]() ,且AO=2OF,
,且AO=2OF,
∴AO=2![]() ,
,
∵AC=![]() ,
,
∴点C是OA的中点,
根据对称性,点D是OE的中点,
∴CD=![]() AE=3,
AE=3,
故答案为:3.

练习册系列答案
相关题目