题目内容
【题目】已知:BC∥OA,∠B=∠A=120°,试回答下列问题:
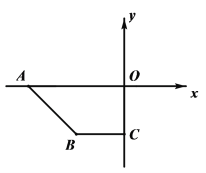
(1)如图1所示,求证:OB∥AC;

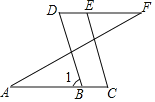
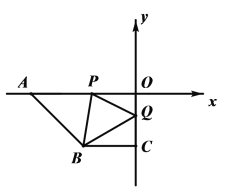
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,则∠EOC的度数是______;

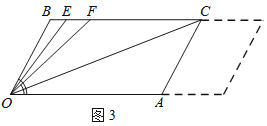
(3)在(2)的条件下,若平行移动AC,其它条件不变,如图3,则∠OCB:∠OFB的值是______.
【答案】(1)证明见解析;(2)30°;(3)1:2
【解析】
(1)依据BC∥OA,即可得到∠A+∠C=180°,根据∠B=∠A,即可得到∠B+∠C=180°,进而得出OB∥AC;
(2)依据BC∥OA,∠B=∠A=120°,即可得到∠AOB=60°,再根据∠FOC=∠AOC,且OE平分∠BOF,即可得出∠EOC=![]() ∠AOB=30°;
∠AOB=30°;
(3)依据BC∥OA,可得∠OCB=∠AOC,∠OFB=∠AOF,再根据∠FOC=∠AOC,即可得到∠AOC:∠AOF=1:2,即∠OCB:∠OFB=1:2.
解:(1)∵BC∥OA,
∴∠A+∠C=180°,
又∵∠B=∠A,
∴∠B+∠C=180°,
∴OB∥AC;
(2)∵BC∥OA,∠B=∠A=120°,
∴∠AOB=60°,
∵∠FOC=∠AOC,且OE平分∠BOF,
∴∠EOF=![]() BOF,∠COF=
BOF,∠COF=![]() ∠AOF,
∠AOF,
∴∠EOC=![]() ∠AOB=30°,
∠AOB=30°,
故答案为:30°;
(3)∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOC:∠AOF=1:2,
∴∠OCB:∠OFB=1:2.
故答案为:1:2.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目