Question

【题目】如图，AB为⊙O的直径，弦CD⊥AB于E，∠CDB=15°，OE=2．

（1）求⊙O的半径；

（2）将△OBD绕O点旋转，使弦BD的一个端点与弦AC的一个端点重合，则弦BD与弦AC的夹角为　 　．

Answer 1

【答案】60°或90°

【解析】试题分析：（1）求出∠BOD的度数，在Rt△ODE中，根据∠DOE=30°，OE=2，求出DE和OD即可；

（2）分为4种情况，分别求出∠CAB和∠OAB（或∠OAD、∠OCB）的度数，相加（或相减）即可求出答案．

试题解析：（1）∵AB为⊙O的直径，弦CD⊥AB于E，

∴，

∴∠BDC=∠BOD，

而∠CDB=15°，

∴∠BOD=2×15°=30°，

在Rt△ODE中，∠DOE=30°，OE=2，

∴OE=DE，OD=2DE，

∴DE==2，

∴OD=4，

即⊙O的半径为4；

（2）有4种情况：如图：

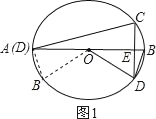
①如图1所示：∵OA=OB，∠AOB=30°，

∴∠OAB=∠OBA=75°，

∵CD⊥AB，AB是直径，

∴弧BC=弧BD，

∴∠CAB=∠BOD=15°，

∴∠CAB=∠BAO+∠CAB=15°+75°=90°；

②如图2所示，∠CAD=75°﹣15°=60°；

③如图3所示：∠ACB=90°；

④如图4所示：∠ACB=60°；

故答案为：60°或90°．