Question

【题目】如图，在平面直角坐标系xOy中，点A（a，0），B（c，c），C（0，c），且满足，P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.

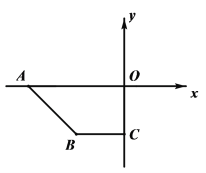
（1）直接写出点B的坐标，AO和BC位置关系是；

（2）当P、Q分别是线段AO，OC上时，连接PB，QB，使，求出点P的坐标；

（3）在P、Q的运动过程中，当∠CBQ=30°时，请探究∠OPQ和∠PQB的数量关系，并说明理由.

Answer 1

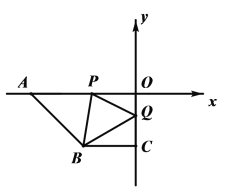
【答案】(1)（-4，-4） ,BC∥AO；（2）P（4，0）;（3）∠PQB =∠OPQ+30°或∠BQP+∠OPQ=150°

【解析】

（1）由解出c，得到B点，易知BC∥AO；

（2）过B点作BE⊥AO于E，设时间经过t秒，AP＝2t，OQ＝t，CQ＝4-t；用t表示出与，根据列出方程解出t即可；

（3）要分情况进行讨论，①当点Q在点C的上方时；过Q点作QH∥AO 如图1所示，利用平行线的性质可得到∠PQB =∠OPQ+30°；

②当点Q在点C的下方时；过Q点作HJ∥AO 如图2所示，同样利用平行线的性质可得到，∠BQP+∠OPQ=150°

(1)由得到c+4=0，得到c=-4

（-4，-4） ,BC∥AO

(2)过B点作BE⊥AO于E

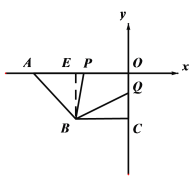
设时间经过t秒，则AP＝2t，OQ＝t，CQ＝4-t

∵BE＝4，BC＝4，

∴·

∵

∴

解得t=2

∴AP＝2t＝4

∴P（4，0）

(3) ①当点Q在点C的上方时；过Q点作QH∥AO 如图一所示，

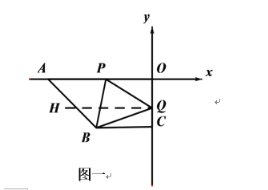
∴∠OPQ=∠PQH.

又∵BC∥AO，QH∥AO

∴QH∥BC

∴∠HQB=∠BCQ=30°.

∴∠OPQ+∠BCQ=∠PQH+∠BQH.

∴即∠PQB =∠OPQ+∠CBQ.

即∠PQB =∠OPQ+30°

②当点Q在点C的下方时；过Q点作HJ∥AO 如图二所示，

∴∠OPQ=∠PQJ.

又∵BC∥AO，QH∥AO

∴QH∥BC

∴∠HQB=∠BCQ=30°.

∴∠HQB+∠BQP+∠PQJ=180°，

∴30°+∠BQP+∠OPQ=180°

即∠BQP+∠OPQ=150°

综上所述∠PQB =∠OPQ+30°或∠BQP+∠OPQ=150°