题目内容
如图⊙O是△ABC的外接圆，圆心O在这个三角形的高AD上，AB=10，BC=12，求⊙O的半径．
如图，连接OB．
∵AD是△ABC的高．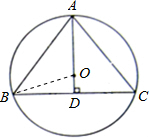
∴BD=
BC=6
在Rt△ABD中，AD=
=
=8．
设圆的半径是R．
则OD=8-R．
在Rt△OBD中，根据勾股定理可以得到：R2=36+（8-R）2
解得：R=
．
∵AD是△ABC的高．
∴BD=
| 1 |
| 2 |
在Rt△ABD中，AD=
| AB2-BD2 |
| 100-36 |
设圆的半径是R．
则OD=8-R．
在Rt△OBD中，根据勾股定理可以得到：R2=36+（8-R）2
解得：R=
| 25 |
| 4 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
试问：（1）中的结论是否成立？并说明理由．