��Ŀ����
����Ŀ����֪�������ϵ�A��C��Ӧ�����ֱ�Ϊa��c��������|a+7|+��c��1��2020��0����B��Ӧ����Ϊ��3��

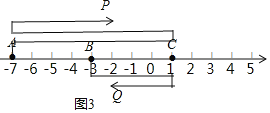
��1��������ͼ��ʾ�������ϱ�ʾ����A��C��Ӧ��λ�ã�
��2��������P��Q�ֱ��A��Bͬʱ���������˶�����P���ٶ�Ϊ3����λ�����룻��Q���ٶ�Ϊ1����λ�����룬��Q�˶�����C����ԭ�ٷ��أ������B��ֹͣ�˶�����P�˶�����C������ԭ�ٷ��أ������A�����۷���C�˶�������Qֹͣ�˶�ʱ��P��ֹ֮ͣ�˶������ڱ���ͼ�л��������˶�����������P��Qͬʱ����������ij��Ĵ���ʾ��ͼ��������õ��������ϱ�ʾ������
���𰸡���1����A��ʾ����Ϊ��7��C���ʾ����Ϊ1����2���������˶�����������P��Qͬʱ����������ij���ʾ����Ϊ��2��0��1��
��������
��1�����÷Ǹ������������a��c��Ȼ���������ϱ�ʾ������
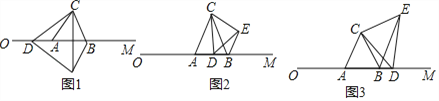
��2����P��Q���˶���ʱ��Ϊt��s��ʱ������AB=4��CB=4��AC=8����P���A����C���˶���Q���B����C���˶�ʱ����ͼ1�������������з���3t-t=4����P���A���˶���C�㣬�۷����ٴ�C����A���˶���Q���B����C���˶�����ͼ2��������������õ�3t-8+t=4����P���A�㵽��C���۷����ٴ�C���˶���A�㣬�����۷���C���˶���Q���B���˶���C��ʱ���۷�����B���˶�����ͼ3��������������õ�3t-16+t-4=8��Ȼ��ֱ�ⷽ�����t���Ӷ��õ��������ʾ������
�⣺��1����|a+7|+��c��1��2020��0��
��a+7��0��c��1��0��
��a����7��c��1��
����A��ʾ����Ϊ��7��C���ʾ����Ϊ1��
��ͼ��
![]()
��2����P��Q���˶���ʱ��Ϊt��s��ʱ������AB����3������7����4��CB��1������3����4��AC��8��
��P���A����C���˶���Q���B����C���˶�ʱ����ͼ1��
3t��t��4�����t��2��
��ʱ�������ʾ����Ϊ��3+t����3+2����1��
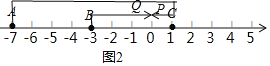
��P���A���˶���C�㣬�۷����ٴ�C����A���˶���Q���B����C���˶�����ͼ2��
3t��8+t��4�����t��3��
��ʱ�������ʾ����Ϊ��3+3t����3+3��0��
��P���A�㵽��C���۷����ٴ�C���˶���A�㣬�����۷���C���˶���Q���B���˶���C��ʱ���۷�����B���˶�����ͼ3��
3t��16+t��4��8�����t��7��
��ʱ�������ʾ����Ϊ��3+4����t��4������2��
���������������˶�����������P��Qͬʱ����������ij���ʾ����Ϊ��2��0��1��