��Ŀ����
����Ŀ����̽����֪������ͼ1������OC�ڡ�AOB���ڲ���ͼ�й���3���ǣ���AOB����AOC�͡�BOC����������һ���ǵĶ�������һ���Ƕ������������������OC�ǡ�AOB�����ɷ�������
��1��һ���ǵ�ƽ������ ������ǵ����ɷ�����������������������������
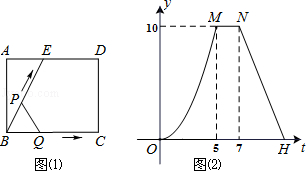
��2����ͼ2������MPN=����������PQ�ǡ�MPN�����ɷ����������MPQ=�� �������ú����Ĵ���ʽ��ʾ�����п��ܵĽ����
�������о�������ͼ2������MPN=60����������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��10�����ٶ���ʱ����ת����PQ��PN��180��ʱֹͣ��ת����ת��ʱ��Ϊt�룮
��3����tΪ��ֵʱ������PM�ǡ�QPN�����ɷ�������
��4��������PMͬʱ�Ƶ�P��ÿ��5�����ٶ���ʱ����ת������PQͬʱֹͣ����ֱ��д��������PQ�ǡ�MPN�����ɷ�����ʱt��ֵ��
���𰸡���1���ǣ���2��![]() ����
����![]() ����
����![]() ������3��tΪ9��12��18ʱ����4��tΪ2.4��4��6.
������3��tΪ9��12��18ʱ����4��tΪ2.4��4��6.
�������������������1�������ɷ��߶��弴���ж�����2������������������ɷ��߶��弴����⣻��3������������������ɷ��߶���õ�������⼴�ɣ���4������������������ɷ��߶���õ�������⼴�ɣ�
���������
��1��һ���ǵ�ƽ����������ǵ����ɷ�����������������������������
�ʴ�Ϊ����
��2���ߡ�MPN=����
���MPQ=![]() ����
����![]() ����
����![]() ����
����
�ʴ�Ϊ![]() ����
����![]() ����
����![]() ����
����
�������
��3����������
��10t=60+![]() ��60��
��60��
���t=9��
��10t=2��60��
���t=12��
��10t=60+2��60��
���t=18��
�ʵ�tΪ9��12��18ʱ������PM�ǡ�QPN�����ɷ�������
��4����������
��10t=![]() ��5t+60����
��5t+60����
���t=2.4��
��10t=![]() ��5t+60����
��5t+60����
���t=4��
��10t=![]() ��5t+60����
��5t+60����
���t=6��
�ʵ�tΪ2.4��4��6ʱ������PQ�ǡ�MPN�����ɷ�������

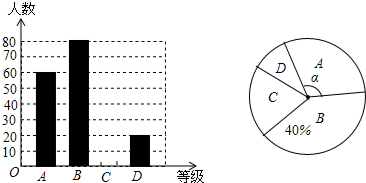
����Ŀ��Ϊ����ͬѧ���˽��Լ�������ˮƽ������1�����������ʦ��ȫ��45��ѧ��������һ������ģ����ԣ��÷־�Ϊ���������ɼ�����Ϊ10�֣�1�������ίԱ������β��Գɼ���������ͳ��ͼ�ͷ��������£�
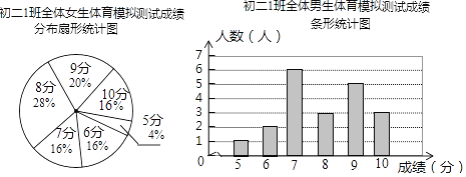
����1������ģ����Գɼ�������
ƽ���� | ���� | ��λ�� | ���� | |
���� | 2 | 8 | 7 | |
�� | 7.92 | 1.99 | 8 |
����������Ϣ������������⣺
��1������������________�ˣ�����Ů��________�ˣ�
��2����ȫ����1������ģ����Գɼ�������.