题目内容
【题目】如图,已知AD∥BC,DC⊥BC, AE平分∠BAD, E为CD中点,试探索AD、BC和AB之间有何关系?并说明理由.
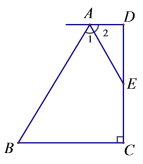
【答案】AD+BC=AB见解析;
【解析】
利用“AAS”可证明Rt△ADE≌Rt△AFE得到AD=AF,利用“HL”可证明Rt△BCE≌Rt△BFE得到BC=BF,于是有AD+BC=AF+BF=AB.
证明:过点E作EF⊥AB,连接BE
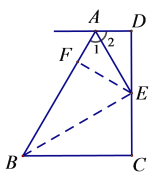
∵AD∥BC,DC⊥BC, EF⊥AB
∴∠D+∠C=180°,∠C=∠AFE=∠BFE=90°
∴∠D=∠AFE =90°.
∵AE平分∠BAD,
∴∠1=∠2
在△ADE和△AFE中
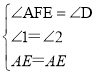
∴△ADE≌△AFE(AAS),
∴FE=DE,AD=AF
又∵E为CD中点
∴DE=CE,
∴FE =CE,
在Rt△BEF和Rt△BEC中,![]()
![]()
∴Rt△ BEF≌Rt△ BEC(HL),
∴BF= BC
∴AD+BC=AF+BF=AB.

练习册系列答案
相关题目