题目内容
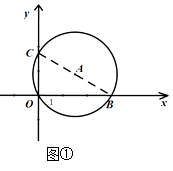
【题目】如图①,在平面直角坐标系中,直径为 ![]() 的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0,
的⊙A经过坐标系原点O(0,0),与x轴交于点B,与y轴交于点C(0, ![]() ).
).
(1)求点B的坐标;
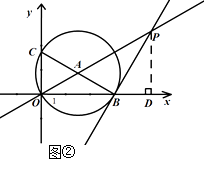
(2)如图②,过点B作⊙A的切线交直线OA于点P,求点P的坐标;
(3)过点P作⊙A的另一条切线PE,请直接写出切点E的坐标.
【答案】
(1)解:如图①,连接 ![]() .
.
∵ ![]() ,
,
∴ ![]() 是⊙
是⊙ ![]() 的直径.
的直径.
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
(2)解:如图②,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() .
.
∵ ![]() 为⊙
为⊙ ![]() 的切线,
的切线,
∴ ![]() .
.
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
(3)解: ![]()
【解析】(1)利用90度圆周角所对的弦是直径,可求出OB即能得出B坐标;(2)先通过P作x轴的垂线构造出横纵坐标对应的线段,利用切线的性质定理和锐角三角函数,求出坐标;(3)如图,利用切线的性质定理和切线长定理得出∠ EPA=30度,PE于x轴平行,连接AE ,求出EF、OF即可求出坐标.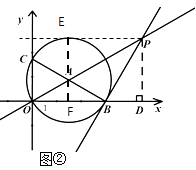
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
相关题目
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元
万元![]() 其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 | 每公顷获利 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
![]() 求出茄子和西红柿的种植面积各为多少公顷?
求出茄子和西红柿的种植面积各为多少公顷?
![]() 种植场在这一季共获利多少万元?
种植场在这一季共获利多少万元?