题目内容
【题目】在△ABC中，AB=AC，点D是BC的中点，点E是AD上任意一点．
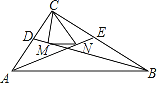
（1）如图1，连接BE、CE，问：BE=CE成立吗？并说明理由；
（2）如图2，若∠BAC=45°，BE的延长线与AC垂直相交于点F时，问：EF=CF成立吗？并说明理由．
【答案】（1）成立．（2）成立．见解析
【解析】
试题分析：（1）成立，根据等腰三角形的性质就可以求出∠BAE=∠CAE，再证明△ABE≌△ACE就可以得出结论；
（2）成立，由BF⊥AC，∠BAC=45°就可以求出AF=BF，在由条件证明△AEF≌△BCF就可以得出结论．
解：（1）成立．
理由：
∵AB=AC，D是BC的中点，∴∠BAE=∠CAE．
在△ABE和△ACE中，
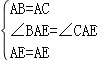
∴△ABE≌△ACE（ SAS ）
∴BE=CE．
（2）成立．
理由：
∵∠BAC=45°，BF⊥AF．
∴△ABF为等腰直角三角形
∴AF=BF…
由（1）知AD⊥BC，
∴∠EAF=∠CBF
在△AEF和△BCF中，
．
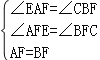∴△AEF≌△BCF（ AAS ），
∴EF=CF．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
【题目】某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如表：
原进价（元/张） | 零售价（元/张） | 成套售价（元/套） | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同．
（1）求表中a的值；
（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售．请问怎样进货，才能获得最大利润？最大利润是多少？
