题目内容
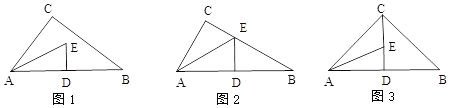
【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
【答案】(1)①30°,②见解析;(2)见解析.
【解析】
(1)由∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E,可直接求出∠B的度数.先证明 BE=2DE,易得BC=3DE
(2) 过点E作EF⊥AC于点F,先证明△ABC是等腰直角三角形△CEF是等腰直角三角形,再证明△ADE≌△AFE(HL)即可.
(1)①∵AE平分∠CAB
∴∠CAE=∠DAE
又∵ED是AB的垂直平分线
∴EA=EB
∴∠B=∠DAE
∴∠CAE=∠DAE=∠B
又∵∠C=90°
∴∠B=![]() ×90°=30°
×90°=30°
②∵AE平分∠CAB,且EC⊥AC,ED⊥AB
∴EC=ED
在Rt△EDB中,∠B=30°
∴BE=2DE
BC=BE+CE=BE+DE=3DE
(2)过点E作EF⊥AC于点F,

∵ED是AB的垂直平分线,且C、E、D共线
∴CD也是AB的垂直平分线
∴CA=CB
又∠ACB=90°
∴△ABC是等腰直角三角形.
∴∠ACD=45°
∴△CEF是等腰直角三角形.
∴EF=CF
∵AE平分∠CAB,且EF⊥AC,ED⊥AB
∴EF=ED
∴ED=FC
在Rt△ADE和Rt△AFE中
EF=ED,AE=AE,
△ADE≌△AFE(HL)
∴AD=AF
∴BC=AC=AF+FC=AD+DE.

练习册系列答案
相关题目