题目内容
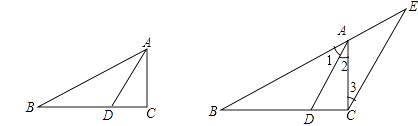
【题目】如图①,在Rt△ABC中,∠C=90°.将△ABC绕点C逆时针旋转得到△A’B’C,旋转角为 ![]() ,且0°<
,且0°< ![]() <180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
<180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
(1)求∠A的度数;
(2)当点C到AA’的距离等于AC的一半时,求 ![]() 的度数.
的度数.
【答案】
(1)解:将 ![]() 绕点
绕点 ![]() 逆时针旋转得到
逆时针旋转得到 ![]() ,旋转角为
,旋转角为 ![]() ,
,
∴ ![]() .
.
∵点 ![]() 可以恰好落在
可以恰好落在 ![]() 的中点处,
的中点处,
∴点 ![]() 是
是 ![]() 的中点.
的中点.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
即 ![]() 是等边三角形.
是等边三角形.
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]()
(2)解:如图,过点 ![]() 作
作 ![]() 于点
于点 ![]() ,
,

点 ![]() 到
到 ![]() 的距离等于
的距离等于 ![]() 的一半,即
的一半,即 ![]() .
.
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() ,即
,即 ![]() .
.
【解析】(1)由旋转性质和直角三角形的斜边中线性质,可先得∠ B = 60 °,再推出∠ A = 30 °;(2)利用30度角的正弦函数,先求出∠ C A D = 30 °,再求出旋转角∠ A C A ' = 120 ° .
【考点精析】利用锐角三角函数的定义和旋转的性质对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目