题目内容
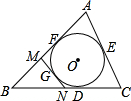
如图，△ABC中，E是△ABC的内心，∠A的平分线和△ABC的外接圆相交于点D，求证：DE=DB．
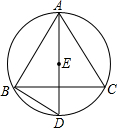
连接BE，
∵E为内心，
∴AE，BE分别为∠BAC，∠ABC的角平分线，
∴∠BED=∠BAE+∠EBA，∠EBA=∠EBC，∠BAE=∠EAC，
∴∠BED=∠EBC+∠EAC，∠EBD=∠EBC+∠CBD，
∵
=
，
∴∠EAC=∠CBD，
∴∠EBD=∠BED，
∴DE=BD．
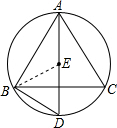
∵E为内心，
∴AE，BE分别为∠BAC，∠ABC的角平分线，
∴∠BED=∠BAE+∠EBA，∠EBA=∠EBC，∠BAE=∠EAC，
∴∠BED=∠EBC+∠EAC，∠EBD=∠EBC+∠CBD，
∵
 |
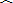| CD |
|
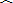| CD |
∴∠EAC=∠CBD，
∴∠EBD=∠BED，
∴DE=BD．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
