题目内容
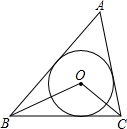
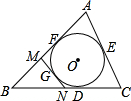
如图，⊙O为△ABC的内切圆，且AB=10，BC=11，AC=7，MN切⊙O于点G，且分别交AB，BC于点M，N，则△BMN的周长是（ ）
| A．10 | B．11 | C．12 | D．14 |
设BF=BD=x，
∵⊙O为△ABC的内切圆，且AB=10，BC=11，AC=7，
∴CD=CE=11-x，AE=AF=10-x，
∴11-x+10-x=7，
解得x=7，
∵MN切⊙O于点G，∴MF=MG，ND=NG，
∴△BMN的周长=BM+BN+MG+NG=BD+BF=2x=14，
故选D．
∵⊙O为△ABC的内切圆，且AB=10，BC=11，AC=7，
∴CD=CE=11-x，AE=AF=10-x，
∴11-x+10-x=7，
解得x=7，
∵MN切⊙O于点G，∴MF=MG，ND=NG，
∴△BMN的周长=BM+BN+MG+NG=BD+BF=2x=14，
故选D．
练习册系列答案
阅读快车系列答案
相关题目
