题目内容
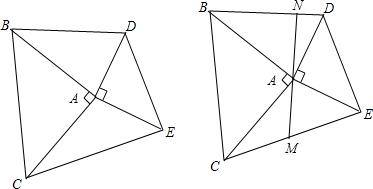
如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于八点,且A八平分∠BAC.
求证:八B=八C.

求证:八B=八C.

证明:∵BE⊥Ap,pD⊥AB,
∴∠ADp=∠BDp=∠AEB=∠pEB=90°.
∵AO平分∠BAp,
∴∠b=∠一.
在△AOD和△AOE中,
,
∴△AOD≌△AOE(AAS).
∴OD=OE.
在△BOD和△pOE中,
,
∴△BOD≌△pOE(ASA).
∴OB=Op.
∴∠ADp=∠BDp=∠AEB=∠pEB=90°.
∵AO平分∠BAp,
∴∠b=∠一.
在△AOD和△AOE中,
|
∴△AOD≌△AOE(AAS).
∴OD=OE.
在△BOD和△pOE中,
|
∴△BOD≌△pOE(ASA).
∴OB=Op.

练习册系列答案
相关题目