题目内容
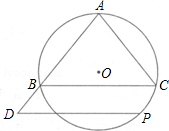
如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是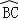 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.
(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.
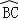 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.

解:(1)当点P是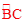 的中点时,DP是⊙O的切线。理由如下:
的中点时,DP是⊙O的切线。理由如下:
连接AP。
∵AB=AC,∴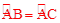 。
。
又∵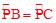 ,∴
,∴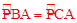 。∴PA是⊙O的直径。
。∴PA是⊙O的直径。
∵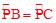 ,∴∠1=∠2。
,∴∠1=∠2。
又∵AB=AC,∴PA⊥BC。
又∵DP∥BC,∴DP⊥PA。∴DP是⊙O的切线。
(2)连接OB,设PA交BC于点E。.
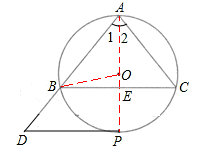
由垂径定理,得BE=BC=6。
在Rt△ABE中,由勾股定理,得:AE=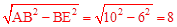 。
。
设⊙O的半径为r,则OE=8﹣r,
在Rt△OBE中,由勾股定理,得:r2=62+(8﹣r)2,解得r=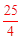 。
。
∵DP∥BC,∴∠ABE=∠D。
又∵∠1=∠1,∴△ABE∽△ADP,
∴ ,即
,即 ,解得:
,解得: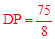 。
。
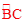 的中点时,DP是⊙O的切线。理由如下:
的中点时,DP是⊙O的切线。理由如下:连接AP。
∵AB=AC,∴
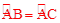 。
。又∵
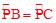 ,∴
,∴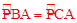 。∴PA是⊙O的直径。
。∴PA是⊙O的直径。∵
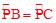 ,∴∠1=∠2。
,∴∠1=∠2。又∵AB=AC,∴PA⊥BC。
又∵DP∥BC,∴DP⊥PA。∴DP是⊙O的切线。
(2)连接OB,设PA交BC于点E。.

由垂径定理,得BE=BC=6。
在Rt△ABE中,由勾股定理,得:AE=
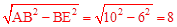 。
。设⊙O的半径为r,则OE=8﹣r,
在Rt△OBE中,由勾股定理,得:r2=62+(8﹣r)2,解得r=
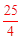 。
。∵DP∥BC,∴∠ABE=∠D。
又∵∠1=∠1,∴△ABE∽△ADP,
∴
 ,即
,即 ,解得:
,解得: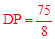 。
。圆心角、弧、弦的关系,圆周角定理,切线的判定,勾股定理,垂径定理,相似三角形的判定和性质。
【分析】(1)根据当点P是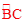 的中点时,得出
的中点时,得出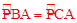 ,得出PA是⊙O的直径,再利用DP∥BC,得出DP⊥PA,问题得证。
,得出PA是⊙O的直径,再利用DP∥BC,得出DP⊥PA,问题得证。
(2)利用切线的性质,由勾股定理得出半径长,进而得出△ABE∽△ADP,即可得出DP的长。
【分析】(1)根据当点P是
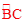 的中点时,得出
的中点时,得出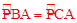 ,得出PA是⊙O的直径,再利用DP∥BC,得出DP⊥PA,问题得证。
,得出PA是⊙O的直径,再利用DP∥BC,得出DP⊥PA,问题得证。(2)利用切线的性质,由勾股定理得出半径长,进而得出△ABE∽△ADP,即可得出DP的长。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在圆O上,
在圆O上,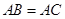 ,
,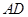 与
与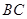 相交于点
相交于点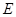 ,
, ,延长
,延长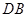 到点
到点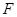 ,使
,使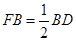 ,连结
,连结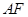 .求证:直线
.求证:直线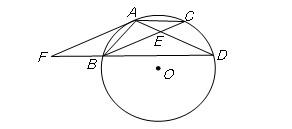
 S△AEO;②AC∥OD;③线段OD是DE与DA的比例中项;④
S△AEO;②AC∥OD;③线段OD是DE与DA的比例中项;④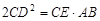 .其中结论正确的是
.其中结论正确的是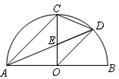
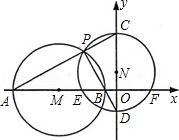
 B.等于4
B.等于4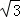 C.等于6 D.随P点
C.等于6 D.随P点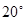 ,弧BD度数为
,弧BD度数为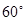 ,则∠P=
,则∠P= 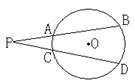
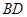 为⊙
为⊙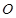 的直径,
的直径,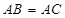 ,
,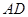 交
交 于点
于点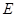 ,
,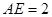 ,
,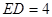 .
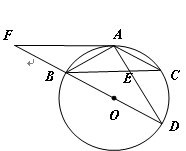
.
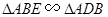 ;
;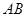 的长;
的长;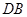 到
到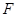 ,使得
,使得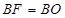 ,连接
,连接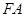 ,试判断直 线
,试判断直 线