题目内容
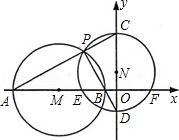
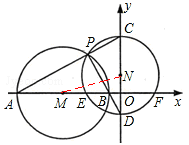
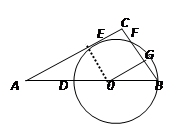
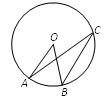
如图,以M(﹣5,0)为圆心、4为半径的圆与x轴交于A.B两点,P是⊙M上异于A.B的一动点,直线PA.PB分别交y轴于C.D,以CD为直径的⊙N与x轴交于E、F,则EF的长【 】
A.等于4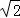 B.等于4
B.等于4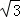 C.等于6 D.随P点
C.等于6 D.随P点

A.等于4
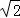 B.等于4
B.等于4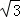 C.等于6 D.随P点
C.等于6 D.随P点C。
圆周角定理,三角形内角和定理,相似三角形的判定和性质,垂径定理,勾股定理。
【分析】 连接NE,设圆N半径为r,ON=x,则OD=r﹣x,OC=r+x,
∵以M(﹣5,0)为圆心、4为半径的圆与x轴交于A.B两点,
∴OA=4+5=9,0B=5﹣4=1。
∵AB是⊙M的直径,∴∠APB=90°。
∵∠BOD=90°,∴∠PAB+∠PBA=90°,∠ODB+∠OBD=90°。
∵∠PBA=∠OBD,∴∠PAB=∠ODB。
∵∠APB=∠BOD=90°,∴△OBD∽△OCA。∴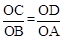 ,即
,即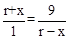 ,即r2﹣x2=9。
,即r2﹣x2=9。
由垂径定理得:OE=OF,
由勾股定理得:OE2=EN2﹣ON2=r2﹣x2=9。∴OE=OF=3,∴EF=2OE=6。
故选C。
【分析】 连接NE,设圆N半径为r,ON=x,则OD=r﹣x,OC=r+x,
∵以M(﹣5,0)为圆心、4为半径的圆与x轴交于A.B两点,

∴OA=4+5=9,0B=5﹣4=1。
∵AB是⊙M的直径,∴∠APB=90°。
∵∠BOD=90°,∴∠PAB+∠PBA=90°,∠ODB+∠OBD=90°。
∵∠PBA=∠OBD,∴∠PAB=∠ODB。
∵∠APB=∠BOD=90°,∴△OBD∽△OCA。∴
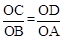 ,即
,即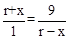 ,即r2﹣x2=9。
,即r2﹣x2=9。由垂径定理得:OE=OF,
由勾股定理得:OE2=EN2﹣ON2=r2﹣x2=9。∴OE=OF=3,∴EF=2OE=6。
故选C。

练习册系列答案
相关题目
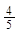 , 求线段AD的长。
, 求线段AD的长。 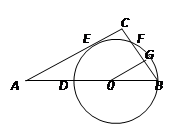
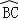 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.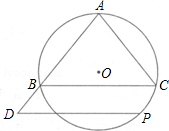
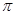
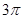
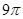
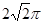
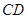 与线段
与线段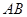 为直径的圆相切于点
为直径的圆相切于点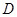 ,并交
,并交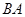 的延长线于点
的延长线于点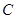 ,且
,且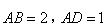 ,
,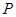 点在切线
点在切线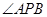 的度数最大时,则
的度数最大时,则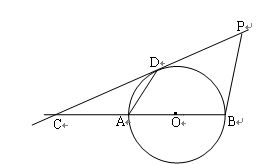
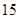 °
°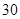 °
°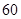 °
°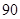 °
°