题目内容
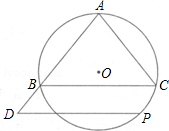
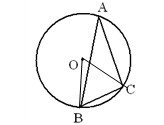
如图,点 在圆O上,
在圆O上,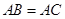 ,
,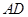 与
与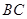 相交于点
相交于点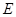 ,
, ,延长
,延长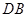 到点
到点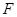 ,使
,使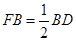 ,连结
,连结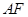 .求证:直线
.求证:直线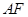 与圆O相切.
与圆O相切.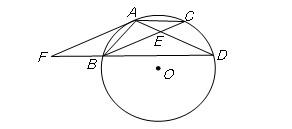
 在圆O上,
在圆O上,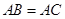 ,
,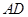 与
与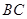 相交于点
相交于点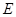 ,
, ,延长
,延长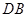 到点
到点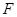 ,使
,使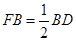 ,连结
,连结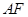 .求证:直线
.求证:直线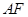 与圆O相切.
与圆O相切.
连OA,如图,

∵AE=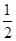 ED,FB=
ED,FB=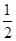 BD,
BD,
∴AE:ED=FB:BD,
∴BE∥AF,
又∵AB=AC,
∴弧AB=弧AC,
∴OA⊥BC,
∴OA⊥AF,
∴直线AF与⊙O相切.

∵AE=
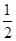 ED,FB=
ED,FB=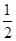 BD,
BD,∴AE:ED=FB:BD,
∴BE∥AF,
又∵AB=AC,
∴弧AB=弧AC,
∴OA⊥BC,
∴OA⊥AF,
∴直线AF与⊙O相切.
连OA,由AE=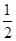 ED,FB=
ED,FB=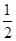 BD,则AE:ED=FB:BD,根据平行线分线段成比例定理得到BE∥AF;由AB=AC,根据垂径定理的推论得到OA⊥BC,则OA⊥AF,根据切线的判定定理即可得到结论.
BD,则AE:ED=FB:BD,根据平行线分线段成比例定理得到BE∥AF;由AB=AC,根据垂径定理的推论得到OA⊥BC,则OA⊥AF,根据切线的判定定理即可得到结论.
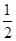 ED,FB=
ED,FB=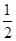 BD,则AE:ED=FB:BD,根据平行线分线段成比例定理得到BE∥AF;由AB=AC,根据垂径定理的推论得到OA⊥BC,则OA⊥AF,根据切线的判定定理即可得到结论.
BD,则AE:ED=FB:BD,根据平行线分线段成比例定理得到BE∥AF;由AB=AC,根据垂径定理的推论得到OA⊥BC,则OA⊥AF,根据切线的判定定理即可得到结论.
练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
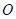 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦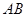 是小圆的切线.若大圆半径为
是小圆的切线.若大圆半径为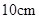 ,小圆半径为
,小圆半径为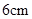 ,则弦
,则弦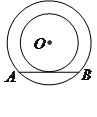
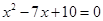 的两个根,O1O2
的两个根,O1O2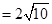 ,则⊙O1和⊙O2的位置关
,则⊙O1和⊙O2的位置关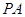 是
是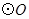 的切线,切点为A,PA=2
的切线,切点为A,PA=2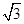 ,∠APO=30°,则
,∠APO=30°,则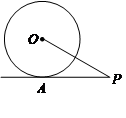
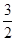 B.2 C.1 D.
B.2 C.1 D.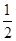

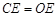 ;③△ODE∽△ADO;④
;③△ODE∽△ADO;④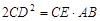 .其中一定正确的结论有( )
.其中一定正确的结论有( )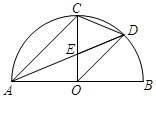
 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.