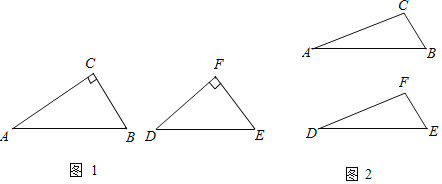[题目]如图.中.是的垂直平分线.是的平分线.为的中位线.连.若.则题目和参考答案——青夏教育精英家教网—

题目内容

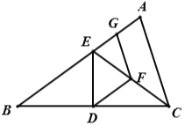
【题目】如图，中，是的垂直平分线，是的平分线，为的中位线，连，若，则_______

【答案】126°

【解析】

利用垂直平分线得到∠EBC=∠ECB=x，再利用外角与中位线性质，求出x的值，再根据∠AEC+∠CED=2x+90-x=90+x求出答案．

解： DE是BC的垂直平分线

BE=CE

设∠EBC=∠ECB=x

∴∠AEC=∠EBC+∠ECB=2x

∵CE平分∠ACB

∴∠BCE=∠ACE=x

∵FG为的中位线

∴FG//AC

∴∠EFG=∠ACE=x

∵D为BC中点，F为CE中点

∴DF//AB

∴∠EFD=∠AEF=2x

∵∠DFG=∠GFE+∠EFD=x+2x=3x

∴3x=108

∴x=36

∴∠AED=∠AEC+∠CED=2x+90-x=90+x=90+36=126．

故答案为：126度．

练习册系列答案

相关题目

【题目】已知抛物线，，，…，（n为正整数），点A(0，1)．

（1）如图1，过点A作y轴垂线，分别交抛物线，，，…，于点，，，…，（和点A不重合）．

①求的长．

②求的长．

（2）如图2，点P从点A出发，沿y轴向上运动，过点P作y轴的垂线，交抛物线于点，，交抛物线于点，，交抛物线于点，，……，交抛物线于点，（在第二象限）．

①求的值．

②求的值．

（3）过x轴上的点Q（原点除外），作x轴的垂线分别交抛物线，，，…，于点，，，…，，是否存在线段（i，j为正整数），使，若存在，求出i＋j的最小值；若不存在，说明理由．

【题目】定义：如果将△ABC与△DEF各分割成两个三角形，且△ABC所分的两个三角形与△DEF所分的两个三角形分别对应相似，那么称△ABC与△DEF互为“近似三角形”，将每条分割线称为“近似分割线”．

（1）如图1，在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，∠A＝30°，∠D＝40°，请判断这两个三角形是否互为“近似三角形”？如果是，请直接在图1中画出一组分割线，并注明分割后所得两个小三角形锐角的度数；若不是，请说明理由．

（2）判断下列命题是真命题还是假命题，若是真命题，请在括号内打“√”；若是假命题，请在括号内打“×”．

①任意两个直角三角形都是互为“近似三角形”　　；

②两个“近似三角形”只有唯一的“近似分割线”　　；

③如果两个三角形中有一个角相等，那么这两个三角形一定是互为“近似三角形”　　．

（3）如图2，已知△ABC与△DEF中，∠A＝∠D＝15°，∠B＝45°，∠E＝60°，且BC＝EF＝，判断这两个三角形是否互为“近似三角形”？如果是，请在图2中画出不同位置的“近似分割线”，并直接分别写出“近似分割线”的和；如果不是，请说明理由．

【题目】在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合（如图1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．

活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD（如图2），当点F与点C重合时停止平移．

（思考）图2中的四边形ABDE是平行四边形吗？请说明理由．

（发现）当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形（如图3）．求AF的长．

活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连结OB，OE（如图4）．

（探究）当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．

【题目】每年的3月15日是“国际消费者权益日”，许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元，在标价8000元的基础上打9折销售.

（1）现在甲卖家欲继续降价吸引买主，问最多降价多少元，才能使利润率不低于20%？

（2）据媒体爆料，有一些卖家先提高商品价格后再降价促销，存在欺诈行为.乙卖家也销售相同的沙发，其成本、标价与甲卖家一致，以前每周可售出8套，现乙卖家先将标价提高，再大幅降价元，使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了，这样一天的利润达到了50000元，求的值.

【题目】某大学生利用40天社会实践参与了某加盟店经营，他销售了一种成本为20元/件的商品，细心的他发现在第天销售的相关数据可近似地用如下表中的函数表示：

销售量	销售单价
	当时，单价为	当时，单价为40

（1）求前20天第几天获得的利润最大？最大利润是多少？

（2）求后20天第几天获得的利润最大？最大利润是多少？

（3）在后20天中，他决定每销售一件商品给山区孩子捐款元（且为整数），此时若还要求每一天的利润都不低于160元，求的值．

【题目】如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．

（1）求证：BG=DE；

（2）若E为AD中点，FH=2，求菱形ABCD的周长．

【题目】珠海市有A，B，C，D，E五个景区很受游客喜爱．对某小区居民在暑假期间去以上五个景区旅游（只选一个景区）的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图．

（1）该小区居民在这次随机调查中被调查到的人数是　　人，m＝　　；

（2）若该小区有居民1500人，试估计去C景区旅游的居民约有多少人？

（3）甲、乙两人暑假打算游玩，甲从B、C两个景点中任意选择一个游玩，乙从B、C 、E三个景点中任意选择一个游玩．求甲、乙恰好游玩同一景点的概率．

【题目】为阻断新冠疫情向校园蔓延，确保师生生命安全和身体健康，教育部通知，2020年春季学期延期开学，利用网上平台，停课不停学”，某校对初三全体学生数学线上学习情况进行调查，随机抽取部分学生的4月月诊断性测试成绩，按由高到低分为A，B，C，D四个等级，根据调查的数据绘制成如下的条形统计图和扇形统计图，请根据图中的信息，解答下列问题：

(1)该校共抽查了　　名同学的数学测试成绩，扇形统计图中A等级所占的百分比a＝　　；

(2)补全条形统计图；

(3)若该校初三共有1180名同学，请估计该校初三学生数学测试成绩优秀（测试成绩B级以上为优秀，含B级）约有　　名；

(4)该校老师想从两男、两女四位学生中随机选择两位了解平时线上学习情况，请用列表或画树形图的方法求出恰好选中一男一女的概率．

试题分类