题目内容
【题目】定义:如果将△ABC与△DEF各分割成两个三角形,且△ABC所分的两个三角形与△DEF所分的两个三角形分别对应相似,那么称△ABC与△DEF互为“近似三角形”,将每条分割线称为“近似分割线”.
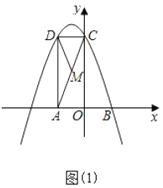
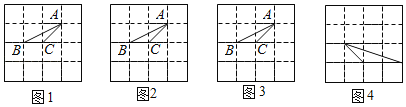
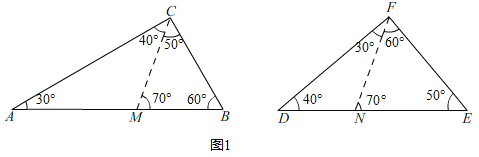
(1)如图1,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,∠A=30°,∠D=40°,请判断这两个三角形是否互为“近似三角形”?如果是,请直接在图1中画出一组分割线,并注明分割后所得两个小三角形锐角的度数;若不是,请说明理由.
(2)判断下列命题是真命题还是假命题,若是真命题,请在括号内打“√”;若是假命题,请在括号内打“×”.
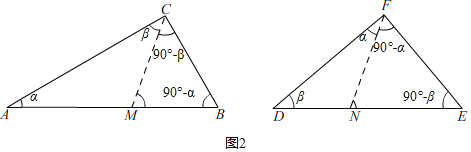
①任意两个直角三角形都是互为“近似三角形” ;
②两个“近似三角形”只有唯一的“近似分割线” ;
③如果两个三角形中有一个角相等,那么这两个三角形一定是互为“近似三角形” .
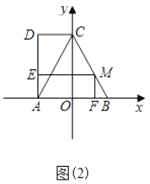
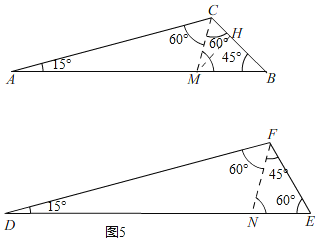
(3)如图2,已知△ABC与△DEF中,∠A=∠D=15°,∠B=45°,∠E=60°,且BC=EF=![]()
![]() ,判断这两个三角形是否互为“近似三角形”?如果是,请在图2中画出不同位置的“近似分割线”,并直接分别写出“近似分割线”的和;如果不是,请说明理由.
,判断这两个三角形是否互为“近似三角形”?如果是,请在图2中画出不同位置的“近似分割线”,并直接分别写出“近似分割线”的和;如果不是,请说明理由.
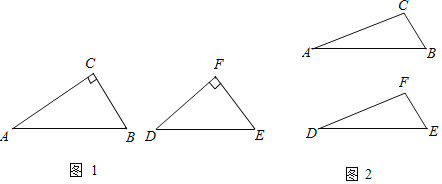
【答案】(1)这两个三角形是互为“近似三角形”,图形见解析;(2)√,×,×;(3)这两个三角形是互为“近似三角形”, “近似分割线”的和为6+4![]() 或
或![]() .
.
【解析】
(1)根据互为“近似三角形”即可得出结论;
(2)根据互为“近似三角形”的意义,判断出是假命题,画图说明即可得出结论;
(3)如图5,先判断出△BCM≌△FEN(ASA),得出CM=FN,再构造出直角三角形,即可得出结论;
②如图6,同(1)的方法即可得出结论.
解:(1)这两个三角形是互为“近似三角形”,如图1所示,
(2)①任意两个直角三角形都是互为“近似三角形”,是真命题,如图2所示,
②两个“近似三角形”只有唯一的“近似分割线”,假命题,如图3所示,
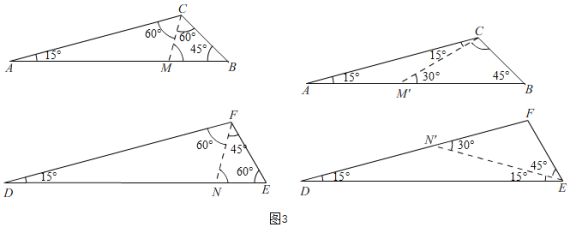
在△ABC与△DEF中,∠A=∠D=15°,∠B=45°,∠E=60°;
③如果两个三角形中有一个角相等,那么这两个三角形一定是互为“近似三角形”,是假命题,
如图4所示,一个顶角为20°的等腰三角形和底角为20°的等腰三角形;
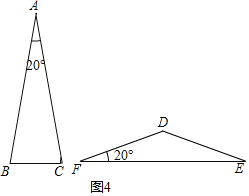 ,
,
故答案为:√,×,×;
(3)这两个三角形是互为“近似三角形”,
①如图5,
在△BCM和△FEN中,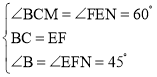 ,
,
∴△BCM≌△FEN(ASA),
∴CM=EN,FN=BM,
过点M作MH⊥BC于H,
在Rt△MHC中,设CH=x,则MH=![]() x,CM=2x,
x,CM=2x,
在Rt△BHM中,BH=MH=![]() x,
x,
∵BC=x+![]() x=
x=![]() ,
,
∴x=![]() ,
,
∴CM=2![]() ,FN=BM=
,FN=BM=![]() ,
,
∴“近似分割线”的和为CM+FN=![]() ;
;
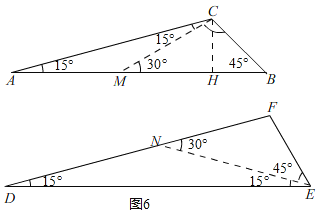
②同①的方法得,△CBM≌FEN(ASA),
∴BM=EN,
过点C作CH⊥BM于H,
在Rt△BHC中,BH=CH=![]() =1+
=1+![]() ,
,
在Rt△CHM中,CM=2CH=2+2![]() ,MH=
,MH=![]() CH=3+
CH=3+![]() ,
,
∴NE=BM=4+2![]() ,
,
∴“近似分割线”的和为CM+EN=6+4![]() ,
,
即“近似分割线”的和为6+4![]() 或
或![]() .
.

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
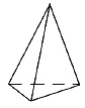
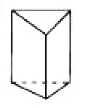
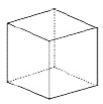
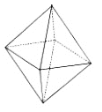
(1)观察下列多面体,并把下表补充完整:
名称 | 三棱锥 | 三棱柱 | 正方体 | 正八面体 |
图形 |
|
|
|
|
顶点数V | 4 | 6 | 8 | |
棱数E | 6 | 12 | ||
面数F | 4 | 5 | 8 |
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.