��Ŀ����
����Ŀ����֪������![]() ��
��![]() ��
��![]() ������
������![]() ��n������������A(0��1)��
��n������������A(0��1)��
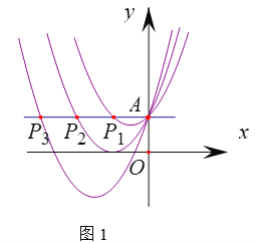
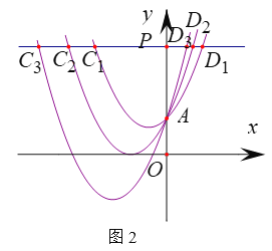
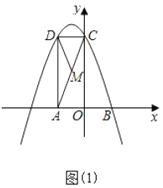
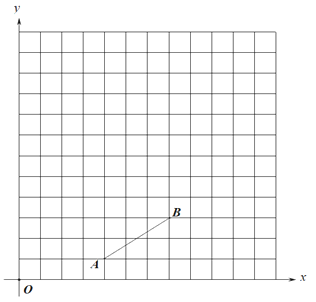
��1����ͼ1������A��y�ᴹ�ߣ��ֱ�������![]() ��
��![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() �͵�A���غϣ���
�͵�A���غϣ���
����![]() �ij���
�ij���
����![]() �ij���
�ij���
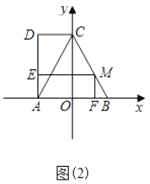
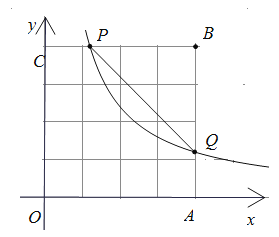
��2����ͼ2����P�ӵ�A��������y�������˶�������P��y��Ĵ��ߣ���������![]() �ڵ�
�ڵ�![]() ��
��![]() ����������
����������![]() �ڵ�
�ڵ�![]() ��
��![]() ����������
����������![]() �ڵ�
�ڵ�![]() ��
��![]() ����������������
����������������![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵڶ����ޣ���
�ڵڶ����ޣ���
����![]() ��ֵ��
��ֵ��
����![]() ��ֵ��
��ֵ��
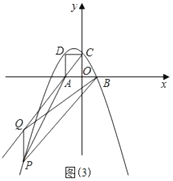
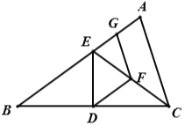
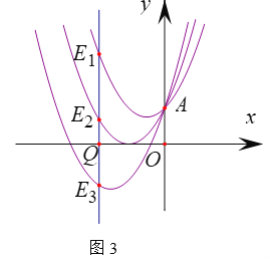
��3����x���ϵĵ�Q��ԭ����⣩����x��Ĵ��߷ֱ�������![]() ��
��![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() ���Ƿ�����߶�
���Ƿ�����߶�![]() ��i��jΪ����������ʹ
��i��jΪ����������ʹ![]() �������ڣ����i��j����Сֵ���������ڣ�˵�����ɣ�
�������ڣ����i��j����Сֵ���������ڣ�˵�����ɣ�
���𰸡���1����1����2020����2����1����2020����3�����ڣ���Сֵ��2022
��������
��1�������ú�������ʽ�ɵõ������ߵĶ������꣬�ٸ��ݶ��κ����ĶԳ��ԣ��ɵõ�P1�ĺ����꣬�Ӷ������AP1��ֵ�������y2��x2��2x��1�ĶԳ��ᣬ���ö��κ��������ʣ��Ϳɵõ���P2�ĺ����꣬�������AP2��ֵ��ͬ���ɵõ�AP3��ֵ����������ɿɵõ�AP2020��ֵ��
��2�������C1�ĺ�����Ϊx1����D1�ĺ�����Ϊx2���ɵõ�PC1����x1��PD1��x2���Ӷ��ɱ�ʾ��PC1��PD1�����ö��κ����ĶԳ��Կɵõ�x1��x2����1������������⣻������ͬ���ķ������PC2��PD2��ֵ����������ɿɵõ�PC2020��PD2020��ֵ��
��3�����Q(x��0)���ɵõ�OQ�ij�����������֪��������������ʽ���ֱ����E1E2��OQ��E1E3��2OQ��E1E4��3OQ����������ɿɵõ�E1En����n��1��OQ������![]() �� �Ϳ����i��j��ֵ��Ȼ����ͼ���.
�� �Ϳ����i��j��ֵ��Ȼ����ͼ���.
��1���⣺��![]() ��
��
��������y1�Ķ�������Ϊ![]() ��
��
��AP1��x�ᣬ
���A�͵�P1���ڶԳ���Գƣ�
���P1�ĺ�����Ϊ![]() ��
��
���P1![]() ��
��
��AP1��|��1��0|��1��
�ڡ�y2��x2��2x��1�ĶԳ���Ϊֱ��![]() �� ��P2�ĺ�����Ϊ��2��
�� ��P2�ĺ�����Ϊ��2��
��AP2��|��2��0|��2��
ͬ����֪��AP3��3��
����
AP2020��2020��
��2���⣺�����C1�ĺ�����Ϊx1����D1�ĺ�����Ϊx2��
��PC1����x1�� PD1��x2��
��PC1��PD1����x1��x2������x1��x2����
������y��x2��x��1�Գ���Ϊֱ��x��![]() �� ��C1�͵�D1���ڶԳ���Գƣ�
�� ��C1�͵�D1���ڶԳ���Գƣ�
��![]() ��
��
��x1��x2����1��
PC1��PD1��������1����1��
�����C2�ĺ�����Ϊx1����D2�ĺ�����Ϊx2��
��PC1����x1��PD1��x2��
��PC2��PD2����x1��x2������x1��x2����
������y��x2��2x��1�Գ���Ϊֱ��x����
��![]() ��
��
��x1��x2����2��
��PC2��PD2��������2����2��
����
PC2020��PD2020��������2020����2020��
��3���⣺���Q��x��0��
��OQ����x��
��E1E2��x2��x��1����x2��2x��1������x��OQ��
E1E3��x2��x��1����x2��3x��1������2x��2OQ��
E1E4��x2��x��1����x2��4x��1������3x��3OQ��
E1En��x2��x��1����x2��nx��1��������1��n��x����n��1��OQ��
��![]() ��
��
��EiEj��2020OQ��
��i��1��j��2020��1��2021��
��i��j����СֵΪ1��2021��2022.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ŷ����Euler��1707��~1783�꣩Ϊ������������ѧ�ҡ���Ȼ��ѧ�ң�������ѧ�����������������������������˽ܳ��Ĺ��ף����Զ����������о������ֶ�����Ķ�������Vertex��������E��Edge��������F��Flat surface��֮�����һ����������ϵ��������������ŷ����ʽ��
��1���۲����ж����壬�����±�����������
���� | ���� | ������ | ������ | �������� |
ͼ�� |
|
|
|
|
������V | 4 | 6 | 8 | |
����E | 6 | 12 | ||
����F | 4 | 5 | 8 |
��2���������е����ݣ����ܷ���V��E��F֮����ʲô��ϵ����д����ϵʽ��____________________________��