题目内容
已知正方形ABCD的边长AB=k(k是正整数),等边三角形PAE的顶点P在正方形内,顶点E在边AB上,且AE="1." 将等边三角形PAE在正方形内按图中所示的方式,沿着正方形的边AB、BC、CD、DA、AB、…连续地翻转n次,使顶点P第一次回到原来的起始位置. ①如果k=1,那么顶点P第一次回到原来的起始位置时,△PAE沿正方形的边连续翻转的次数n= ;②如果顶点P第一次回到原来的起始位置时,等边三角形PAE沿正方形的边连续翻转的次数是84,那么正方形ABCD的边长k= .

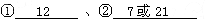
(1)正△PAE的顶点P在正方形内按图1中所示的方式连续地翻转,顶点P第一次回到原来的起始位置,实际上正方形周长和与三角形的周长和相等,正方形的周长=4k,三角形的周长=3,即找4k,3的最小公倍数,由此求出k=1,2,3时n的值;故当k是3的倍数时,n=4k;当k不是3的倍数时,n=12k.
(2)根据当k是3的倍数时,n=4k;当k不是3的倍数时,n=12k即可求得k的值.
解答:解:正△PAE的顶点P在正方形内按图1中所示的方式连续地翻转,顶点P第一次回到原来的起始位置,实际上正方形周长和与三角形的周长和相等,正方形的周长=4k,三角形的周长=3,即找4k,3的最小公倍数;
(1)当k=1时,4k,3的最小公倍数是12,故n=12;
(2)当k不是3的倍数时,84=12×7,则k=7;
当k是3的倍数时:84=4×21,则k=21.
(2)根据当k是3的倍数时,n=4k;当k不是3的倍数时,n=12k即可求得k的值.
解答:解:正△PAE的顶点P在正方形内按图1中所示的方式连续地翻转,顶点P第一次回到原来的起始位置,实际上正方形周长和与三角形的周长和相等,正方形的周长=4k,三角形的周长=3,即找4k,3的最小公倍数;
(1)当k=1时,4k,3的最小公倍数是12,故n=12;
(2)当k不是3的倍数时,84=12×7,则k=7;
当k是3的倍数时:84=4×21,则k=21.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 , ∠B=90°.
, ∠B=90°.




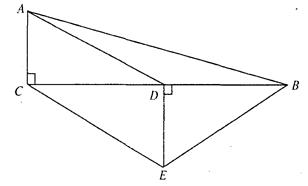
 满分6分)如图,在△ABC中,∠ACB=90°,D是BC中点,DE⊥BC,CE∥AD,若AC=2,CE=4.求四边形ACEB的周长.
满分6分)如图,在△ABC中,∠ACB=90°,D是BC中点,DE⊥BC,CE∥AD,若AC=2,CE=4.求四边形ACEB的周长.