题目内容
如图,在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.正确的个数是

A.4 B.3 C.2 D.1

A.4 B.3 C.2 D.1
B
①∵点B′与点B关于AE对称,
∴△ABF与△AB′F关于AE对称,
∴AB=AB′,
∵AB=AD,
∴AB′=AD.故本选项正确;
②如图,连接EB′.

则BE=B′E=EC,
∠FBE=∠FB′E,
∠EB′C=∠ECB′.
则∠FB′E+∠EB′C=∠FBE+∠ECB′=90°,
即△BB′C为直角三角形.
∵FE为△BCB′的中位线,
∴B′C=2FE,
∵△B′EF∽△AB′F,
∴
 ,
,故FB′=2FE.
∴B′C=FB′.
∴△FCB′为等腰直角三角形.
故本选项正确.
③假设∠ADB′=75°成立,
则∠AB′D=75°,
∠ABB′=∠AB′B=360°-75°-75°-90°=60°,
∴△ABB′为等边三角形,
故B′B=AB=BC,与B′B<BC矛盾,
故本选项错误.
④设∠ABB′=∠AB′B=x度,
∠AB′D=∠ADB′=y度,
则在四边形ABB′D中,2x+2y+90=360,
即x+y=135度.
又∵∠FB′C=90°,
∴∠DB′C=360°-135°-90°=135°.
故本选项正确.
故选B.

练习册系列答案
相关题目
 的边长为1,
的边长为1,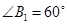 ;作
;作 于点
于点 ,以
,以 为一边,做第二个菱形
为一边,做第二个菱形 ,使
,使 ;作
;作 于点
于点 ,以
,以 为一边做第三个菱形
为一边做第三个菱形 ,使
,使 ;
; 依此类推,这样做的第
依此类推,这样做的第 个菱形
个菱形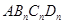 的边
的边 的长是_____________.
的长是_____________.

 ,若AC=AB=2,BD= .
,若AC=AB=2,BD= .





