题目内容
【题目】已知AB是⊙O的直径,C为⊙O上一点,OC=4,∠OAC=60°.
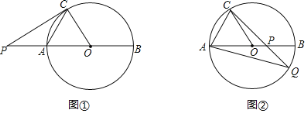
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
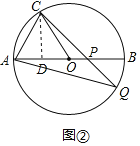
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小及PA的长.
【答案】(Ⅰ)30°;(Ⅱ)45°;2+![]()
【解析】
(Ⅰ)根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形,得出∠AC=OC=4,AOC=60°,根据切线的性质得出∠OCP=90°,进而求得∠P=∠ACP=30°;
(Ⅱ)作CD⊥AB于D,根据圆周角定理求得∠Q=30°,根据等腰三角形的性质求得∠QAC=∠QCA=75°,∠OAC=∠OCA=60°,即可求得∠QAO=∠QCO=15°,根据三角形外角的性质求得∠APC=45°,得出△PCD是等腰直角三角形,解直角三角形求得CD,AD,即可求得PA.
解:(Ⅰ)∵OA=OC,∠OAC=60°,
∴△AOC是等边三角形,
∴AC=OC=4,∠AOC=60°,
∵过点C作⊙O的切线,与BA的延长线交于点P,
∴∠OCP=90°,
∴∠P=∠ACP=30°;
(Ⅱ)作CD⊥AB于D,
∵∠AOC=60°,
∴∠Q=30°,
∵AQ=CQ,
∴∠QAC=∠QCA=75°,
∵∠OAC=∠OCA=60°,
∴∠QAO=∠QCO=15°,
∵∠AOC=∠POC+∠APC,
∴∠APC=60°-15°=45°,
∴△PCD是等腰直角三角形,
∴PD=CD,
∵CD=![]() AC=
AC=![]() ,AD=
,AD=![]() AC=2,
AC=2,
∴PD=![]() ,
,
∴PA=AD+PD=2+![]() .
.

练习册系列答案
相关题目