题目内容
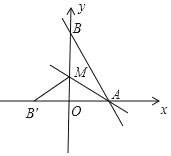
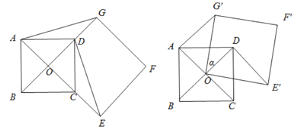
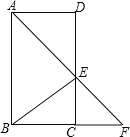
【题目】如图,将两块直角三角板摆放在平面直角坐标系中,有![]() ,
,![]() ,
, ![]() ,且
,且![]() .现将
.现将![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]()
![]() .在旋转过程中,直线
.在旋转过程中,直线![]() 分别与直线
分别与直线![]() ,
,![]() 交于点
交于点![]() ,
,![]() .
.
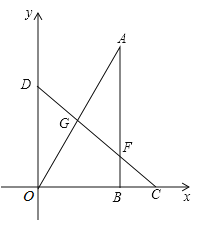
(1)当旋转角![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)在旋转过程中,当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)在旋转过程中,![]() 能否为等腰是三角形?若能,请求出所有满足条件的
能否为等腰是三角形?若能,请求出所有满足条件的![]() 值;若不能,请说明理由.
值;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)当
;(3)当![]() 为
为![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
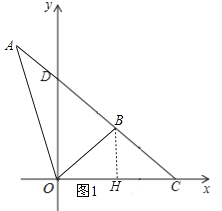
(1)过点B作BH⊥x轴于点H,在Rt△AOB中,∠AOB=60°,OA=8,所以![]() ,再利用勾股定理求出OH、BH,即可解答;
,再利用勾股定理求出OH、BH,即可解答;
(2)分两种情况:Ⅰ当点B在第一象限时(如图2),过点B作BM⊥OC于点M;Ⅱ当点B在第二象限时(如图3),过点B作BE⊥x轴于E,过点A作AF⊥BE于H;分别求出点A、B的坐标,利用待定系数法求解析式,即可解答;
(3)分三种情况:Ⅰ当0°<β<45°时(如图4);Ⅱ当45°<β<75°时(如图5);Ⅲ当75°<β<180°时,分三种情况解答:①FA=FG,②AF=AG,③GA=GF;根据等腰三角形的性质,角之间的和与差,即可解答.
解;(1)如图1,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴∠OAB=30°
![]() .
.
当![]() ,即
,即![]() 时,则
时,则![]() .
.
![]() .
.
![]() .
.
![]() .
.
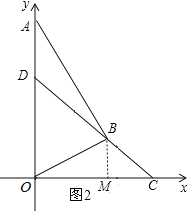
(2)①当点![]() 在第一象限时,如图2,过点
在第一象限时,如图2,过点![]() 作
作![]() 于点
于点![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]()
![]() 点
点![]() 在
在![]() 轴上,
轴上,
![]() .
.
设直线![]() 的解析式为
的解析式为![]()
由题意,得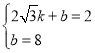 ,
,
解得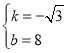 .
.
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
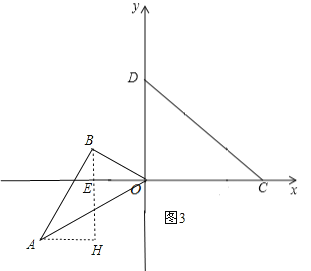
②当点![]() 在第二象限时,如图3,过点
在第二象限时,如图3,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的延长线于点
的延长线于点![]() .
.
![]() ,
,![]() .
.
![]()
![]()
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,
![]()
又![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() .
.
![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
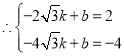 ,
,
解得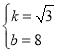
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
综上所述,直线![]() 的解析式为
的解析式为![]() 或
或![]() .
.
(3)由题意可知,当![]() 时,可证得
时,可证得![]() .
.
![]() 分为以下情况讨论:
分为以下情况讨论:
I当![]() 时,如图4,则
时,如图4,则![]() 为钝角.
为钝角.
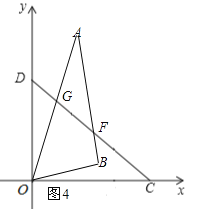
当![]() 时,有
时,有![]() .
.
![]()
又![]() ,
,![]() .
.
![]()
II当![]() 时,如图5,则
时,如图5,则![]() 为钝角.
为钝角.
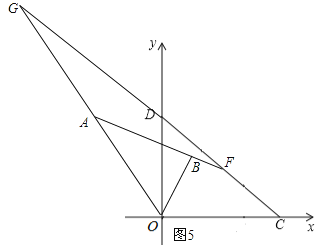
当![]() 时,
时,![]() .
.
![]()
![]()
III当![]() 时,
时,
①若![]() ,如图6,有
,如图6,有![]()
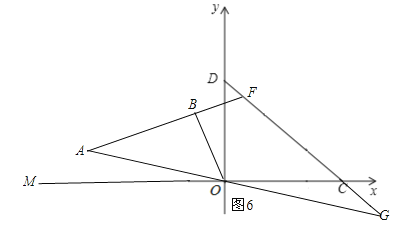
![]() .
.
![]()
②若![]() ,如图7,有
,如图7,有![]()
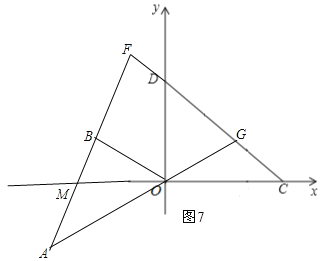
![]()
![]() .
.
![]() .
.
③若![]() ,如图8,有
,如图8,有![]() .
.
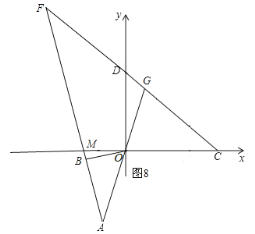
![]() .
.
![]() ,
,![]() (舍去).
(舍去).
综上所述,当![]() 为
为![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

 名校课堂系列答案
名校课堂系列答案