��Ŀ����
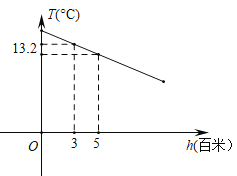
����Ŀ����������С�ӷֱ�������ֿ�����ͬ�Ĺ���Ч�ʵ���һ�����ʣ�����ͬʱ��ʼ�������ڶ�С�ӹ���5������ڼ�����������豸5�죬Ϊ���Ͻ��ȣ��ٴο��������ǽ�����Ч����ߵ�ԭ�ȵ�2��������͵�һС��ͬʱ������������ӵ������ʵĹ����У������ֿ����ʵ�ʣ����y t���һС�ӹ���ʱ��x��ĺ���ͼ����ͼ��ʾ��

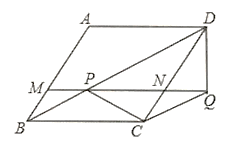
��1�������߶�AC����ʾ��y��x֮��ĺ�������ʽ��
�����F�����꣬�����͵�F��ʵ�����壮
��2������ڶ�С��û�м����豸����ԭ���Ĺ���Ч��������������ô������������������ �죮
���𰸡���1����y����30x��360���ڵ�F������Ϊ��8��120������F��ʵ�������ǣ���һС�ӹ���8��������ֿ�ʣ������ʶ�Ϊ120 t����2��9��
��������
��1�����ô���ϵ������⼴�ɣ�
�ڸ��ݵ�һС�ӵĹ���Ч������ڶ�С���ٴο�����Ĺ���Ч�ʣ����ɵõ���F�������꣬�������н���ʽ���������F���꣬�������֪��F��ʵ�������ǣ���һС�ӹ���8��������ֿ�ʣ������ʶ�Ϊ120 t��
��2�����ݹ���Ч���Լ���F�������꣬����������豸������»���Ҫ���������������Ӽ���.
�⣺��1���⣺����AC�ĺ�������ʽΪy��kx��b������12��0������0��360������y��kx��b���ɵ�![]() ��
��
��y����30x��360��
�ڵ�һС�ӵĹ���Ч��Ϊ360��12��30��t���죩��
�ڶ�С���ٴο�����Ĺ���Ч��Ϊ30��2��60��t���죩����������Ϊ60��2��120��t����
����E������Ϊ��10��120�������Ե�F��������Ϊ120��
��y��120����y����30x��360���ɵ�x��8������F������Ϊ��8��120����
��F��ʵ�������ǣ���һС�ӹ���8��������ֿ�ʣ������ʶ�Ϊ120 t��
��2���ߵڶ�С�ӹ���5��ֿ�ʣ�������Ϊ120 t ��
��120��30��4���죩��
4+5=9���죩��
������ڶ�С��û�м����豸����ԭ���Ĺ���Ч��������������ô������������������9�죮

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�