题目内容
【题目】如图，已知点A是双曲线
在第一象限的分支上的一个动点，连接AO并延长交另一分支于点B，过点A作y轴的垂线，过点B作x轴的垂线，两垂线交于点C，随着点A的运动，点C的位置也随之变化．设点C的坐标为（m，n），则m，n满足的关系式为（ ）
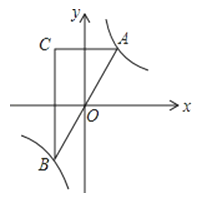
A.n=﹣2m
B.n=
C.n=﹣4m
D.n=
【答案】B
【解析】解：由反比例函数的性质可知，A点和B点关于原点对称，
∵点C的坐标为（m，n），
∴点A的坐标为（
，n），
∴点B的坐标为（﹣，﹣n），
根据图象可知，B点和C点的横坐标相同，
∴﹣=m，即n=﹣
．
故选：B．
首先根据点C的坐标为（m，n），分别求出点A的坐标、点B的坐标；然后根据AO、BO所在的直线的斜率相同，求出m，n满足的关系式即可．
练习册系列答案
相关题目
