题目内容
【题目】已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3)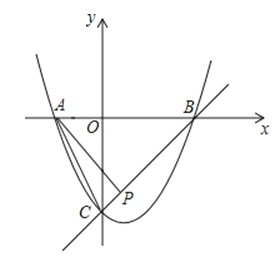
(1)求抛物线的函数表达式.
(2)求直线BC的函数表达式和∠ABC的度数.
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
【答案】
(1)
解:将点A的坐标(﹣1,0),点C的坐标(0,﹣3)代入抛物线解析式得:
![]() ,
,
解得:![]() ,
,
故抛物线解析式为:y=x2﹣2x﹣3;
(2)
解:由(1)得:0=x2﹣2x﹣3,
解得:x1=﹣1,x2=3,故B点坐标为:(3,0),
设直线BC的解析式为:y=kx+d,
则![]() ,
,
解得:![]() ,
,
故直线BC的解析式为:y=x﹣3,
∵B(3,0),C(0,﹣3),
∴BO=OC=3,
∴∠ABC=45°;
(3)
解:过点P作PD⊥x轴于点D,
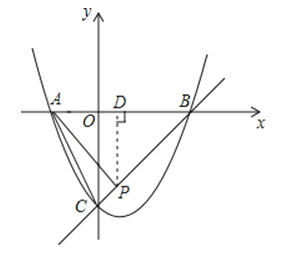
∵∠ACB=∠PAB,∠ABC=∠PBA,
∴△ABP∽△CBA,
∴![]() =
=![]() ,
,
∵BO=OC=3,
∴BC=3![]() ,
,
∵A(﹣1,0),B(3,0),
∴AB=4,
∴![]() =
=![]() ,
,
解得:BP=![]() ,
,
由题意可得:PD∥OC,
∴DB=DP=![]() ,
,
∴OD=3﹣![]() =
=![]() ,
,
则P(![]() ,﹣
,﹣![]() ).
).
【解析】(1)直接将A,C点坐标代入抛物线解析式求出即可;
(2)首先求出B点坐标,进而利用待定系数法求出直线BC的解析式,进而利用CO,BO的长求出∠ABC的度数;
(3)利用∠ACB=∠PAB,结合相似三角形的判定与性质得出BP的长,进而得出P点坐标.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

 天天向上口算本系列答案
天天向上口算本系列答案【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表: 该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题: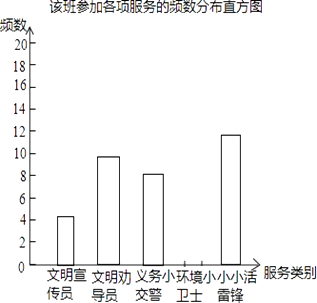
(1)该班参加这次公益活动的学生共有名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.
【题目】某市准备将一批帐篷和食品送往扶贫区.已知帐篷和食品共320件,且帐篷比食品多80件.
(1)直接写出帐篷有 件,食品有 件;
(2)现计划租用A、B两种货车共8辆,一次性将这批物资全部送到扶贫区,已知两种车可装帐篷和食品的件数以及每辆货车所需付运费情况如表,问:共有几种租车的方案?最少运费是多少?
帐篷(件) | 食品(件) | 每辆需付运费(元) | |
A种货车 | 40 | 10 | 780 |
B种货车 | 20 | 20 | 700 |