题目内容
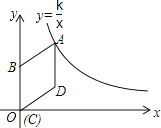
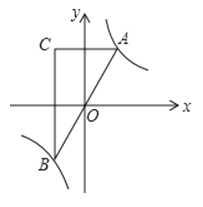
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣![]() x+3交AB,BC于点M,N,反比例函数y=
x+3交AB,BC于点M,N,反比例函数y=![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
【答案】
(1)
解:∵B(4,2),四边形OABC是矩形,
∴OA=BC=2,
将y=2代入y=﹣![]() x+3得:x=2,
x+3得:x=2,
∴M(2,2),
把M的坐标代入y=![]() 得:k=4,
得:k=4,
∴反比例函数的解析式是y=![]() ;
;
(2)
解:把x=4代入y=![]() 得:y=1,即CN=1,
得:y=1,即CN=1,
∵S四边形BMON=S矩形OABC﹣S△AOM﹣S△CON
=4×2﹣![]() ×2×2﹣
×2×2﹣![]() ×4×1=4,
×4×1=4,
由题意得:![]() |OP|×AO=4,
|OP|×AO=4,
∵AO=2,
∴|OP|=4,
∴点P的坐标是(4,0)或(﹣4,0).
【解析】(1)求出OA=BC=2,将y=2代入y=﹣![]() x+3求出x=2,得出M的坐标,把M的坐标代入反比例函数的解析式即可求出答案;
x+3求出x=2,得出M的坐标,把M的坐标代入反比例函数的解析式即可求出答案;
(2)求出四边形BMON的面积,求出OP的值,即可求出P的坐标
此题考查了反比例函数的应用,根据条件求出点坐标进而求出反比例函数解析式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目