题目内容
【题目】(1)求证:三角形三个内角的和等于180°.
(2)阅读材料并回答问题:
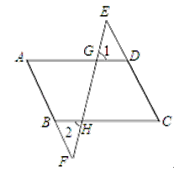
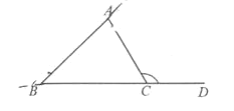
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的“外角”,在每个顶点处取这个三角形的一个外角,它们的和叫做这个三角形的“外角和”.补全图形并求△ABC的“外角和”.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)过A点作MN∥BC,根据平行线的性质及平角的定义解答.
(2)结合三角形的内角和与平角的定义求解即可.
(1)过A点作MN∥BC,
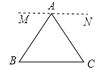
∴∠MAB=∠B,∠NAC=∠C (同位角相等)
∵∠MAB+∠BAC+∠NAC=180°
∴∠B+∠BAC+∠C=180°
∴三角形的内角和为180°
(2)如图:
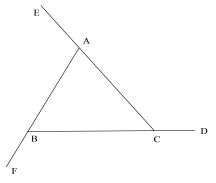
∵∠ACD+∠ACB=180°,∠EAF+∠BAC=180°,∠FBC+∠ABC=180°
∴∠ACD+∠ACB+∠EAF+∠BAC+∠FBC+∠ABC=540°
∵∠ABC+∠BAC+∠ACB=180°
∴∠ACD+∠EAF+∠FBC=360°
即三角形的外角和等于360°

练习册系列答案
相关题目