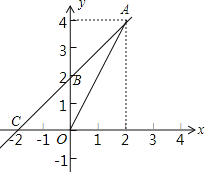题目内容
【题目】(【材料阅读】阅读下列一段文字,然后回答下列问题.
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:
MN=![]() .
.
例如:已知P(3,1)、Q(1,﹣2),则这两点间的距离PQ=![]() =
=![]() .
.
【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
(3)如图,在平面直角坐标系xOy中,二次函数y=x2﹣4的图象与x轴相交于两点A、B,(点A在点B的左边)
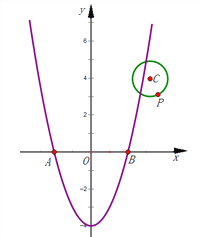
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心、1为半径的圆上一动点,求PA2+PB2的最大值;
【答案】(1)AB=10; (2)△ABC是直角三角形;(3)①A(-2,0)B(2,0);②80.
【解析】分析:(1)依据两点间的距离公式可求得AB的长;(2)依据两点间的距离公式可求得AB、AC、BC的长,然后依据勾股定理的逆定理可对△ABC的形状作出判断;(3)①令y=0得:x-4=0,解得x=2或x=-2,故此可得到A,B的坐标;②首先依据两点间的距离公式表示出PA+PB的长,通过化简可得到PA+PB=2PO+8,然后求得OP的最大值,从而可得到问题的答案.
本题解析:
(1)AB=10;
(2)△ABC是直角三角形;
(3)①A(-2,0)B(2,0)
②PA2+PB2=![]() =
=![]()
当PO过圆心C时,PO最大为OC+PC=5+1=6
因此PA2+PB2最大值为![]()

练习册系列答案
相关题目