��Ŀ����
����Ŀ����ģ�ͽ�����
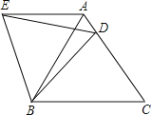
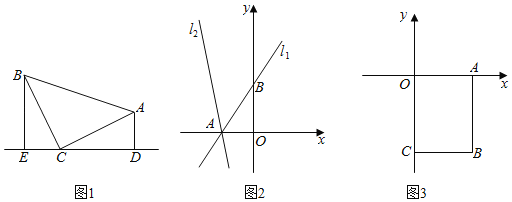
��1����ͼ1������Rt��ABC�У���ACB��90����CB��CA��ֱ��ED������C������A��AD��ED�ڵ�D������B��BE��ED�ڵ�E����֤����BEC�ա�CDA��
��ģ��Ӧ�ã�
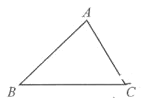
��2����ͼ2����ֱ֪��l1��y��![]() x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��l1�Ƶ�A��ʱ����ת45����ֱ��l2����ֱ��l2�ĺ�������ʽ��
x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��l1�Ƶ�A��ʱ����ת45����ֱ��l2����ֱ��l2�ĺ�������ʽ��
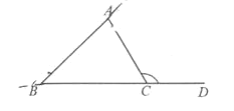
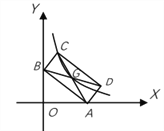
��3����ͼ3��ƽ��ֱ������ϵ����һ��B��3����4��������B��BA��x���ڵ�A��BC��y���ڵ�C����P���߶�AB�ϵĶ��㣬��D��ֱ��y����2x+1�ϵĶ������ڵ��������ڣ���̽����CPD�ܷ��Ϊ����ֱ�������Σ����ܣ������D�����꣬�����ܣ���˵�����ɣ�
���𰸡���1������⣻��2��![]() ����3����D����ã�
����3����D����ã�![]() ��
��![]() ����4��
����4��![]() 7����
7����![]() ��
��![]() ����
����
��������
��1���ɴ�ֱ�Ķ���á�ADC=��CEB=90����ƽ�ǵĶ����ͬ�ǵ���ǵ���������DAC=��ECB���ǽDZ�֤����CDA�ա�BEC��
��2��֤����ABO�ա�BCD�������C������Ϊ��-3��5�����ɵ㵽ֱ���Ϲ�����Ԫһ�η��������k=![]() 5��b=
5��b=![]() 10������ϵ�������ֱ��l2�ĺ�������ʽΪy=-5x-10��
10������ϵ�������ֱ��l2�ĺ�������ʽΪy=-5x-10��
��3��������MCP�ա�HPD���������ʣ���D��ֱ��y=-2x+1���m=![]() ��n=0��
��n=0��![]() ����m��ֵ���룬�õ�D����ã�
����m��ֵ���룬�õ�D����ã�![]() ��
��![]() ����4��
����4��![]() 7����
7����![]() ��
��![]() ����
����
�⣺��1����ͼ1��ʾ��
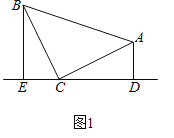
��AD��ED��BE��ED��
���ADC=��CEB=90����
�֡ߡ�ACD+��ACB+��BEC=180������ACB=90����
���ACD+��BEC=90����
�֡ߡ�ACD+��DAC=90����
���DAC=��ECB��
����CDA����BEC��
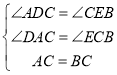 ��
��
���CDA�ա�BEC��AAS����
��2������B��BC��AB��AC�ڵ�C��CD��y�ύy���ڵ�D����ͼ2��ʾ��
��CD��y�ᣬx���y�ᣬ
���CDB=��BOA=90����
�֡�BC��AB��
���ABC=90����
�֡ߡ�ABO+��ABC+��CBD=180����
���ABO+��CBD=90����
�֡ߡ�BAO+��ABO=90����
���BAO=��CBD��
�֡ߡ�BAC=45����
���ACB=45����
��AB=CB��
����ABO�͡�BCD�У�
 ��
��
���ABO�ա�BCD��AAS����
��AO=BD��BO=CD��
�֡�ֱ��l1��y=![]() x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
���A��B���������ֱ�Ϊ��-2��0������0��3����
��AO=2��BO=3��
��BD=2��CD=3��
���C��������-3��5����
��l2�ĺ�������ʽΪy=kx+b��k��0����
��A��C������ֱ��l2�ϣ�������ã�
![]() ��
��
��![]() ��
��
��ֱ��l2�ĺ�������ʽΪy=![]() 5x
5x![]() 10��
10��
��3���ܳ�Ϊ����ֱ�������Σ�������ã�
������PΪֱ��ʱ����ͼ3����ʾ��
���P������Ϊ��3��m������PB�ij�Ϊ4+m��
�ߡ�CPD=90����CP=PD��
��CPM+��CDP+��PDH=180����
���CPM+��PDH=90����
�֡ߡ�CPM+��DPM=90����
���PCM=��PDH��
����MCP����HPD��
 ��
��
���MCP�ա�HPD��AAS����
��CM=PH��PM=PD��
���D��������7+m��-3+m����
�֡ߵ�D��ֱ��y=-2x+1�ϣ�
��-2��7+m��+1=-3+m��
��ã�m=![]() ��
��
����D��������![]() ��
��![]() ����
����
������CΪֱ��ʱ����ͼ3����ʾ��
���P������Ϊ��3��n������PB�ij�Ϊ4+n��
CA=CD��
ͬ����֤����PCM�ա�CDH��AAS����
��PM=CH��MC=HD��
���D��������4+n��-7����
�֡ߵ�D��ֱ��y=-2x+1�ϣ�
��-2��4+n��+1=-7��
��ã�n=0��
���P���A�غϣ���M���O�غϣ�
����D��������4��-7����
������DΪֱ��ʱ����ͼ3����ʾ��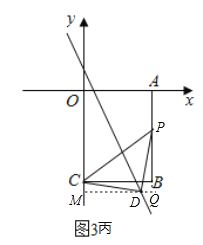
���P������Ϊ��3��k������PB�ij�Ϊ4+k��
CD=PD��
ͬ����֤����CDM�ա�PDQ��AAS����
��MD=PQ��MC=DQ��
���D��������![]() ��
��![]() ����
����
�֡ߵ�D��ֱ��y=-2x+1�ϣ�
��-2��![]() +1=
+1=![]() ��
��
��ã�k=![]() ��
��
���P���A�غϣ���M���O�غϣ�
����D��������![]() ��
��![]() ����
����
�ۺ���������D����ã�![]() ��
��![]() ����4��
����4��![]() 7����
7����![]() ��
��![]() ����
����