题目内容
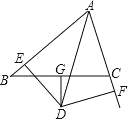
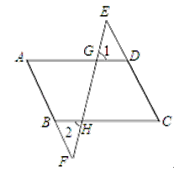
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空(理由或数学式):
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A
∴AB∥CD( )
【答案】见解析.
【解析】
先根据同位角相等,两直线平行,判定AD∥BC,进而得到∠ADE=∠C,再根据内错角相等,两直线平行,即可得到AB∥CD.
证明:∵∠1=∠2(已知)
∠1=∠AGH(对顶角相等)
∴∠2=∠AGH(等量代换)
∴AD∥BC(同位角相等,两直线平行)
∴∠ADE=∠C(两直线平行,同位角相等)
∵∠A=∠C(已知)
∴∠ADE=∠A
∴AB∥CD(内错角相等,两直线平行)
故答案为:已知;对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;内错角相等,两直线平行.

【题目】某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
销售额(万元) | 17 | 19 | 20 | 21 | 25 | 26 | 28 | 30 |
频数(人数) | 1 | 1 | 3 | 3 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
【题目】阅读下列材料: 某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
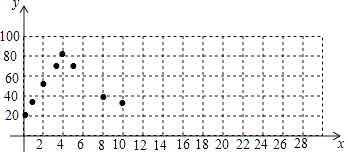
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式; 当4<x≤16时,写出一个符合表中数据的函数解析式;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min.