��Ŀ����
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ�������ɽ��ʡ�����ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣�ij�̳��ƻ������ף������ֽ��ܵƹ�1200ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���
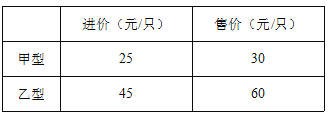
(1)��ν�����������ǡ��Ϊ46000Ԫ?
(2)���̳��������ֽ��ܵ�xֻ������̳���������ܵ�ʱ������w�빺�����ֽ��ܵ�x֮��ĺ�����ϵʽ��
(3)��ν������̳���������ܵ�ʱ��������Ҳ����������۵�30%����ʱ����Ϊ����Ԫ?
���𰸡���1���������ͽ��ܵ�400ֻ�����ͽ��ܵ�800ֻ����2��w=��10x+18000����3���̳��������ͽ��ܵ�450ֻ�����ͽ��ܵ�750ֻ����������ܵ�ʱ����Ϊ13500Ԫ��
��������
��1�����̳�Ӧ�������ͽ��ܵ�xֻ�����������г����̽�ɣ�
��2�����̳�Ӧ�������ͽ��ܵ�xֻ�����������г���������ʽ���ɣ�
��3�����̳��������ͽ��ܵ�xֻ�������ͽ��ܵƣ�1200��x��ֻ�����ݡ��̳���������ܵ�ʱ��������Ҳ����������۵�30%���в���ʽ�����һ�κ��������ʽ�ɣ�
��1�����̳�Ӧ�������ͽ��ܵ�xֻ�������ͽ��ܵ�Ϊ��1200��x��ֻ����������ã�
25x+45��1200��x��=46000
��ã�x=400��
��x=400ʱ��1200��x=800��
�𣺹������ͽ��ܵ�400ֻ�����ͽ��ܵ�800ֻʱ��������ǡ��Ϊ46000Ԫ��
��2�����̳�Ӧ�������ͽ��ܵ�xֻ���̳��������������ܵƿɻ���wԪ��
��������ã�w=��30��25��x+��60��45����1200��x��=5x+18000��15x=��10x+18000
����w=��10x+18000��
��3�����̳��������ͽ��ܵ�xֻ�������ͽ��ܵƣ�1200��x��ֻ������ΪwԪ����������ã�
��10x+18000��[25x+45��1200��x��]��30%
��ã�x��450��
��w=��10x+18000����k=��10��0����w��x���������С����x=450ʱ��w���=13500Ԫ��
���̳��������ͽ��ܵ�450ֻ���������ͽ��ܵ�750ֻʱ���������Ϊ13500Ԫ��