ƒøƒ⁄»ð
°æƒø°ø‘ƒ∂¡œ¬¡–≤ƒ¡œ£¨Ω‚æˆÃ·≥ˆµƒŒ £∫
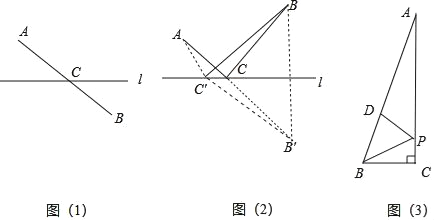
◊Ó∂ì∑æ∂Œ Â:»ÁÕº£®1£©£¨µ„A£¨B∑÷± «÷±œþl“Ï≤ýµƒ¡Ω∏ˆµ„£¨»Á∫Œ‘⁄÷±œþl…œ’“µΩ“ª∏ˆµ„C£¨ πµ√µ„CµΩµ„A£¨µ„Bµƒæý¿Î∫Õ◊Ó∂ãøŒ“√«÷ª–Ë¡¨Ω”AB£¨”Î÷±œþlœýΩª”⁄“ªµ„£¨ø…÷™’‚∏ˆΩªµ„º¥Œ™À˘«Û£Æ
»ÁÕº£®2£©£¨»Áπ˚µ„A£¨B∑÷± «÷±œþlÕ¨≤ýµƒ¡Ω∏ˆµ„£¨»Á∫Œ‘⁄l…œ’“µΩ“ª∏ˆµ„C£¨ πµ√’‚∏ˆµ„µΩµ„A°¢µ„Bµƒæý¿Î∫Õ◊Ó∂ãøŒ“√«ø…“‘¿˚”√÷·∂‘≥∆µƒ–‘÷ £¨◊˜≥ˆµ„Bπÿ”⁄µƒ∂‘≥∆µ„B£¨’‚ ±∂‘”⁄÷±œþl…œµƒ»Œ“ªµ„C£¨∂º±£≥÷CB£ΩCB£¨¥”∂¯∞—Œ £®2£©±‰Œ™Œ £®1£©£Æ“Ú¥À£¨œþ∂ŒAB”Î÷±œþlµƒΩªµ„CµƒŒª÷√º¥Œ™À˘«Û£Æ
Œ™¡ÀÀµ√˜µ„CµƒŒª÷√º¥Œ™À˘«Û£¨Œ“√«≤ª∑¡‘⁄÷±œþ…œ¡ÌÕ‚»Œ»°“ªµ„C°‰£¨¡¨Ω”AC°‰£¨BC°‰£¨B°‰C°‰£Æ“ÚŒ™AB°‰°ÐAC°‰+C°‰B°‰£¨°ýAC+CB£ºAC'+C°‰B£¨º¥AC+BC◊Ó–°£Æ
»ŒŒÒ£∫
˝—ßÀºøº
£®1£©≤ƒ¡œ÷–ªÆœþ≤ø∑÷µƒ“¿æð «°° °°£Æ
£®2£©≤ƒ¡œ÷–Ω‚æˆÕº£®2£©À˘ æŒ Ã‚ÃÂœ÷µƒ ˝—ßÀºœÎ «°° °°£Æ£®ÃÓ◊÷ƒ∏¥˙∫≈º¥ø…£©
A£Æ◊™ªØÀºœÎ
B£Æ∑÷¿ýÃ÷¬€ÀºœÎ
C£Æ’˚ÃÂÀºœÎ
«®“∆”¶”√
£®3£©»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œC£Ω90°„£¨°œBAC£Ω15°„£¨µ„PŒ™C±þ…œµƒ∂ص„£¨µ„DŒ™AB±þ…œµƒ∂ص„£¨»ÙAB£Ω8cm£¨‘ÚBP+DPµƒ◊Ó–°÷µŒ™°° °°cm£Æ
°æ¥∞∏°ø£®1£©¡Ωµ„÷ƺ‰œþ∂Œ◊Ó∂êڻ˝Ω«–Œµƒ¡Ω±þ÷Æ∫Õ¥Û”⁄µ⁄»˝±þ£ª£®2£©A£ª£®3£©4
°æΩ‚Œˆ°ø
£®1£©“¿æð «¡Ωµ„÷ƺ‰œþ∂Œ◊Ó∂êڻ˝Ω«–Œµƒ¡Ω±þ÷Æ∫Õ¥Û”⁄µ⁄»˝±þ£ª
£®2£©≤ƒ¡œ÷–Ω‚æˆÕº£®2£©À˘ æŒ Ã‚ÃÂœ÷µƒ ˝—ßÀºœÎ «◊™ªØµƒÀºœÎ£ª
£®3£©»ÁÕº£®3£©÷–£¨◊˜µ„Bπÿ”⁄µ„Cµƒ∂‘≥∆µ„B°‰£¨¡¨Ω”AB°‰£Æ◊˜BH°ÕAB°‰”⁄H£Æ◊˜µ„Dπÿ”⁄ACµƒ∂‘≥∆µ„D°‰£¨‘ÚPD£ΩPD°‰£¨Õ∆≥ˆPB+PD£ΩPB+PD°‰£¨∏˘æð¥πœþ∂Œ◊Ó∂Ãø…÷™£¨µ±µ„D°‰”ÎH÷ÿ∫œ£¨B£¨P£¨D°‰π≤œþ ±£¨PB+PDµƒ◊Ó–°÷µ£Ωœþ∂ŒBHµƒ≥§£ª
£®1£©≤ƒ¡œ÷–ªÆœþ≤ø∑÷µƒ“¿æð «¡Ωµ„÷ƺ‰œþ∂Œ◊Ó∂êڻ˝Ω«–Œµƒ¡Ω±þ÷Æ∫Õ¥Û”⁄µ⁄»˝±þ£ª
π ¥∞∏Œ™£∫¡Ωµ„÷ƺ‰œþ∂Œ◊Ó∂êڻ˝Ω«–Œµƒ¡Ω±þ÷Æ∫Õ¥Û”⁄µ⁄»˝±þ£ª
£®2£©≤ƒ¡œ÷–Ω‚æˆÕº£®2£©À˘ æŒ Ã‚ÃÂœ÷µƒ ˝—ßÀºœÎ «◊™ªØµƒÀºœÎ£¨
π ¥∞∏Œ™A£Æ
£®3£©»ÁÕº£®3£©÷–£¨◊˜µ„Bπÿ”⁄µ„Cµƒ∂‘≥∆µ„B°‰£¨¡¨Ω”AB°‰£Æ◊˜BH°ÕAB°‰”⁄H£Æ

◊˜µ„Dπÿ”⁄ACµƒ∂‘≥∆µ„D°‰£¨‘ÚPD£ΩPD°‰£¨
°ýPB+PD£ΩPB+PD°‰£¨
∏˘æð¥πœþ∂Œ◊Ó∂Ãø…÷™£¨µ±µ„D°‰”ÎH÷ÿ∫œ£¨B£¨P£¨D°‰π≤œþ ±£¨PB+PDµƒ◊Ó–°÷µ£Ωœþ∂ŒBHµƒ≥§£¨
°þBC£ΩCB°‰£¨AC°ÕBB°‰£¨
°ýAB£ΩAB°‰£¨
°ý°œBAC£Ω°œCAB°‰£Ω15°„£¨
°ý°œBAH£Ω30°„£¨
‘⁄Rt°˜ABH÷–£¨°þAB£Ω8cm£¨°œBAH£Ω30°„£¨
°ýBH£Ω![]() AB£Ω4cm£¨
AB£Ω4cm£¨
°ýPB+PDµƒ◊Ó–°÷µŒ™4cm£Æ
π ¥∞∏Œ™4£Æ

°æƒø°ø¡–∑Ω≥ÃΩ‚”¶”√Â
ƒ≥÷–—ß∆þƒÍº∂![]() ¡Ω∏ˆ∞ýπ≤105»À£¨“™»• –ø∆ºº≤©ŒÔπðΩ¯––…Áª·¥ÛøŒÃ√ªÓ∂Ø£¨¿œ ¶÷∏≈…–°√˜µΩÕ¯…œ≤È‘ƒ∆±º€–≈œ¢£¨–°√˜≤ȵ√∆±º€»Áœ¬±Ì£∫∆‰÷–∆þ
¡Ω∏ˆ∞ýπ≤105»À£¨“™»• –ø∆ºº≤©ŒÔπðΩ¯––…Áª·¥ÛøŒÃ√ªÓ∂Ø£¨¿œ ¶÷∏≈…–°√˜µΩÕ¯…œ≤È‘ƒ∆±º€–≈œ¢£¨–°√˜≤ȵ√∆±º€»Áœ¬±Ì£∫∆‰÷–∆þ![]() ∞ý≤ª◊„50»À£¨æ≠π¿À„£¨»Áπ˚¡Ω∏ˆ∞ý∂º“‘∞ýŒ™µ•Œªπ∫∆±£¨“ªπ≤”¶∏∂1140‘™£Æ
∞ý≤ª◊„50»À£¨æ≠π¿À„£¨»Áπ˚¡Ω∏ˆ∞ý∂º“‘∞ýŒ™µ•Œªπ∫∆±£¨“ªπ≤”¶∏∂1140‘™£Æ
π∫∆±’≈ ˝ | √ø’≈∆±µƒº€∏Ò |
| 12 |
| 10 |
100“‘…œ | a |
£®1£©¡Ω∏ˆ∞ý∏˜”–∂ý…Ÿ—ß…˙£ø
£®2£©»Áπ˚¡Ω∏ˆ∞ý¡™∫œ∆¿¥£¨◊˜Œ™“ª∏ˆÕ≈ÃÂπ∫∆±£¨ø…“‘ °300‘™£¨«Î«Ûaµƒ÷µ£Æ