题目内容
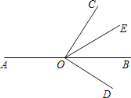
【题目】某景区在同一线路上顺次有三个景点A，B，C，甲、乙两名游客从景点A出发，甲步行到景点C；乙花20分钟时间排队后乘观光车先到景点B，在B处停留一段时间后，再步行到景点C．甲、乙两人离景点A的路程s（米）关于时间t（分钟）的函数图像如图所示．
（1）甲的速度是 米/分钟；
（2）当20≤t ≤30时，求乙离景点A的路程s与t的函数表达式；
（3）乙出发后多长时间与甲在途中相遇？
（4）若当甲到达景点C时，乙与景点C的路程为360米，则乙从景点B步行到景点C的速度是多少？
【答案】（1）60；（2）s＝300t－6000；（3）乙出发5分钟和30分钟时与甲在途中相遇；（4）乙从景点B步行到景点C的速度是68米/分钟．
【解析】
（1）观察图像得出路程和时间，即可解决问题．
（2）利用待定系数法求一次函数解析式即可；
（3）分两种情况讨论即可；
（4）设乙从B步行到C的速度是x米/分钟，根据当甲到达景点C时，乙与景点C的路程为360米，所用的时间为（90-60）分钟，列方程求解即可．
（1）甲的速度为
60米/分钟．
（2）当20≤t ≤30时，设s=mt＋n，由题意得：
，解得：
，所以s=300t－6000；
（3）①当20≤t ≤30时，60t=300t－6000，解得：t=25，25－20=5；
②当30≤t ≤60时，60t=3000，解得：t=50，50－20=30．
综上所述：乙出发5分钟和30分钟时与甲在途中相遇．
（4）设乙从B步行到C的速度是x米/分钟，由题意得：
5400－3000－（90－60） x=360
解得：x=68．
答：乙从景点B步行到景点C的速度是68米/分钟．
阅读快车系列答案
【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质，并解决问题．
(1)完成下列步骤，画出函数y=|x|的图象；
①列表、填空；
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描点；
③连线．
(2)观察图象，当x 时，y随x的增大而增大；
(3)根据图象，不等式|x|＜
x+
的解集为 ．
