Question

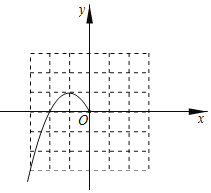
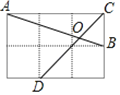
【题目】如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则cos∠AOD=___．

Answer 1

【答案】

【解析】

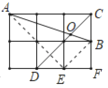
设右下角顶点为点F，取DF的中点E，连接BE，AE，由点B为CF的中点、点E为DF的中点可得出BE∥CD，进而可得出∠AOD＝∠ABE，在△ABE中，由AB2＝AE2＋BE2可得出∠AEB＝90°，再利用余弦的定义即可求出cos∠ABE的值，此题得解．

解：设右下角顶点为点F，取DF的中点E，连接BE，AE，如图所示．
∵点B为CF的中点，点E为DF的中点，
∴BE∥CD，
∴∠AOD＝∠ABE．
在△ABE中，AB＝，AE＝2，BE＝，
∵AB2＝AE2＋BE2，
∴∠AEB＝90°，
∴cos∠ABE＝＝
∴cos∠AOD＝
故答案为：.