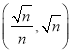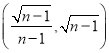Question

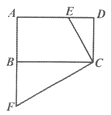
【题目】如图，在正方形ABCD中，点E与点F分别在线段AC、BC上，且四边形DEFG是正方形。

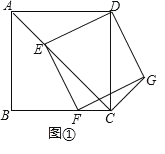
(1)求证AE=CG，并说明理由。

(2)连接AG，若AB=17，DG=13，求AG的长.

Answer 1

【答案】（1）AE=CG;（2）3

【解析】

(1)因为四边形EFGD是正方形，所以DE=DG,∠EDC+∠CDG=90°，由四边形ABCD是正方形，得到∠ADE=∠CDG，根据全等三角形的判定（SAS）得到△ADE≌△CDG，再根据全等三角形的性质得到AE=CG；

（2）由（1）知，AE=CG，又因为∠DCG=∠DAE=45°，结合题意得到∠ACG=90°，

所以得到AE⊥CG，过E作EH⊥AD，设AH=EH=x，则根据勾股定理得到，解得x=5，则AE=CG=5，故可得AG=3.

(1)理由是：如图1，∵四边形EFGD是正方形，

∴DE=DG,∠EDC+∠CDG=90°，

∵四边形ABCD是正方形，

∴AD =CD,∠ADE+∠EDC=90°，

∴∠ADE=∠CDG，

∴△ADE≌△CDG（SAS），

∴AE=CG.

（2）由（1）知，AE=CG，又∠DCG=∠DAE=45°，

∵∠ACD=45°，

∴∠ACG=90°，

∴CG⊥AC，即AE⊥CG，

过E作EH⊥AD，设AH=EH=x，则

解得x=5，则AE=CG=5，

所以AG==3.