Question

【题目】利用函数图象探究方程x（|x|﹣2）＝的实数根的个数．

（1）设函数y＝x（|x|﹣2），则这个函数的图象与直线y＝的交点的横坐标就是方程x（|x|﹣2）＝的实数根．

（2）分类讨论：当x≤0时，y＝﹣x2﹣2x；当x＞0时，y＝　 　；

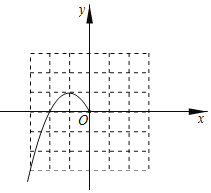
（3）在给定的坐标系中，已经画出了当x≤0时的函数图象，请根据（2）中的解析式，通过描点，连线，画出当x＞0时的函数图象．

（4）在给定的坐标系中画直线y＝、观察图象可知方程x（|x|﹣2）＝的实数根有　 　个．

（5）深入探究：若关于x的方程2x（|x|﹣2）＝m有三个不相等的实数根，且这三个实数根的和为负数，则m的取值范围是　 　．

Answer 1

【答案】（1）函数y＝x（|x|﹣2）的图象与直线y＝的交点的横坐标就是方程x（|x|﹣2）＝的实数根；（2）x2﹣2x；（3）如图，见解析；（4）3；（5）﹣2≤m＜0．

【解析】

（1）函数y＝x（|x|﹣2）的图象与直线y＝的交点的横坐标就是方程x（|x|﹣2）＝的实数根．

（2）根据绝对值的性质去掉绝对值整理即可，注意x的取值范围；

（3）通过描点，连线，画出当x＞0时的函数图象即可；

（4）根据两个函数图象交点的个数，找出方程解的个数；

（5）根据两个函数图象相交产生的交点，比较交点横坐标的特征，加以分析即可求得．

解：（1）函数y＝x（|x|﹣2）的图象与直线y＝的交点的横坐标就是方程x（|x|﹣2）＝的实数根．

（2）当x＞0时，y＝x（|x|﹣2）＝x（x﹣2）＝x2﹣2x，

故答案为x2﹣2x；

（3）如图：

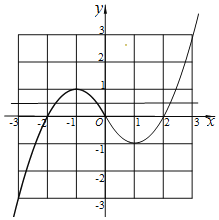
（4）如（3）题图，直线y＝的图象与y＝x（|x|﹣2）的图象有三个交点，则可知方程x（|x|﹣2）＝的实数根有 3个．

故答案为3；

（5）根据题意画出图象：

直线y＝m与函数y＝x（|x|﹣2）的交点的横坐标x1＜0＜x2＜x3，且x2+x3＝2，x1≤﹣2，

∴x1+x2+x3≤0，

∴﹣2≤m＜0

∴关于x的方程x（|x|﹣2）＝即2x（|x|﹣2）＝m有三个不相等的实数根，且这三个实数根的和为非负数，则m的取值范围是﹣2≤m＜0，

故答案为﹣2≤m＜0．