题目内容
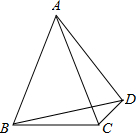
如图，在△ABC中，∠ABD=∠ACD=60°，∠ADB=90°-
∠BDC．
求证：△ABC是等腰三角形．
| 1 |
| 2 |
求证：△ABC是等腰三角形．
证明：∵∠ABD=∠ACD，
∴A、B、C、D四点共圆，
∴∠ADB=∠ACB，∠BDC=∠BAC，
∵∠ADB=90°-
∠BDC，
∴∠ACB=90°-
∠BAC，
∴2∠ACB+∠BAC=180°
又∵∠ABC+∠ACB+∠BAC=180°
∴∠ABC=∠ACB，
∴AB=AC，
∴△ABC是等腰三角形．
∴A、B、C、D四点共圆，
∴∠ADB=∠ACB，∠BDC=∠BAC，
∵∠ADB=90°-
| 1 |
| 2 |
∴∠ACB=90°-
| 1 |
| 2 |
∴2∠ACB+∠BAC=180°
又∵∠ABC+∠ACB+∠BAC=180°
∴∠ABC=∠ACB，
∴AB=AC，
∴△ABC是等腰三角形．
练习册系列答案
阅读快车系列答案
相关题目
