题目内容
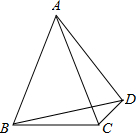
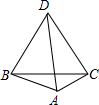
在凸四边形ABCD中,DA=DB=DC=BC,则这个四边形中最大角的度数是( )
| A.120° | B.135° | C.150° | D.165° |

解;设∠CDA=x,∠ABC=y,
∵DA=DB=DC=BC,
∴∠BDC=∠DBC=∠DCB=60°,
∠DBA=∠DAB,∠DAC=∠DCA,
∵∠DBA+∠BAD+∠BDA=180°,
∴60°-x+2(60°+y)=180°,
即x=2y,
∠BAC=360°-∠DBA-∠DCA-∠BDC,
=360°-(60°+y)-
-60°,
=150°.
故选C.
∵DA=DB=DC=BC,
∴∠BDC=∠DBC=∠DCB=60°,
∠DBA=∠DAB,∠DAC=∠DCA,
∵∠DBA+∠BAD+∠BDA=180°,
∴60°-x+2(60°+y)=180°,
即x=2y,
∠BAC=360°-∠DBA-∠DCA-∠BDC,
=360°-(60°+y)-
| 180°-2y |
| 2 |
=150°.
故选C.

练习册系列答案
相关题目