Question

【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）

（1）若△A1B1C1与△ABC关于y轴成轴对称，则△A1B1C1三个顶点坐标分别为A1_____，B1_____，C1_____

（2）在y轴上是否存在点Q．使得S△ACQ=S△ABC，如果存在，求出点Q的坐标，如果不存在，说明理由；

（3）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标是_____．

Answer 1

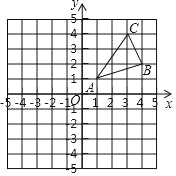
【答案】（﹣1，1） （﹣4，2） （﹣3，4） （2，0）

【解析】

（1）作出A、B、C关于y轴的对称点A′、B′、C′即可；

（2）存在．设Q（0，m），构建方程即可解决问题；

（3）如图作点B关于x轴的对称点B′，连接AB′交x轴于P，此时PA+PB的值最小；

（1）△A1B1C1如图所示，A1（﹣1，1），B1（﹣4，2），C1（﹣3，4）．

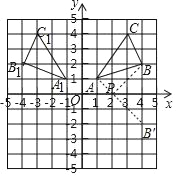
故答案为（﹣1，1），（﹣4，2），（﹣3，4）．

（2）存在．设Q（0，m），

∵S△ABC=9﹣×2×3﹣×3×1﹣×1×2=，

∴S△QAC=，

∴|m|3﹣|m|1=，

∴m=±，

∴Q（0，）或（0，﹣）．

（3）如图作点B关于x轴的对称点B′，连接AB′交x轴于P，此时PA+PB的值最小，此时P（2，0）．