题目内容
【题目】如图所示，直线AB与x轴交于点A，与y轴交于点C（0，2），且与反比例函数y=﹣ 
的图象在第二象限内交于点B，过点B作BD⊥x轴于点D，OD=2． 
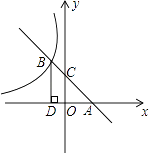
（1）求直线AB的解析式；
（2）若点P是线段BD上一点，且△PBC的面积等于3，求点P的坐标．
【答案】
（1）解：OD=2，B点的横坐标是﹣2，
当x=﹣2时，y=﹣ 
=4，
∴B点坐标是（﹣2，4），
设直线AB的解析式是y=kx+b，图象过（﹣2，4）、（0，2），
，
解得 
，
∴直线AB的解析式为y=﹣x+2
（2）解：∵OD=2， 
=3，
∴BP=3，
PD=BD﹣BP=4﹣3=1，
∴P点坐标是（﹣2，1）
【解析】（1）根据图象上的点满足函数解析式，可得B点坐标，根据待定系数法，可得函数解析式；（2）三角形的面积公式，BP的长，可得P点坐标．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
【题目】小明购买了一部新手机，到某通讯公司咨询移动电话资费情况，准备办理入网手续，该通讯公司工作人员向他介绍两种不同的资费方案：
方案代号 | 月租费（元） | 免费时间（分） | 超过免费时间的通话费（元/分） |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
（1）分别写出方案一、二中，月话费（月租费与通话费的总和）y（单位：元）与通话时间x（单位：分）的函数关系式；
（2）画出（1）中两个函数的图象；
（3）若小明月通话时间为200分钟左右，他应该选择哪种资费方案最省钱．
