题目内容
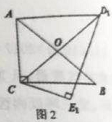
【题目】已知在四边形ABCD中，∠A=90°，AB=3，AD=4，BC=12，CD=13，求四边形ABCD的面积.
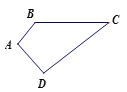
【答案】36
【解析】
试题根据勾股定理求得BD=5；由勾股定理的逆定理判定△BCD为直角三角形，则四边形ABCD的面积=△ABD的面积+△BCD的面积．
试题解析：∵在△ABD中，∠A是直角，AB=3，AD=4，
∴由勾股定理得 BD2=AD2+AB2=25．则BD=5，
又∵在△BCD中，BC=12，DC=13，
∴CD2=BD2+BC2=169，
∴△BCD为直角三角形，且∠DBC=90°，
∴S四边形ABCD=S△ABD+S△BCD=
ADAB+BDBC=×4×3+×5×12=36．
即四边形ABCD的面积是36．
考点: 1.勾股定理；2.勾股定理的逆定理．
练习册系列答案
相关题目
【题目】九年级数学兴趣小组经过市场调查，得到某种图书每月的销售与售价的关系为函数关系如下表：
售价（元/本） | 50 | 55 | 60 | 65 | … |
月销量（本） | 2000 | 1800 | 1600 | 1400 | … |
已知该图书的进价为每本30元，设售价为x元．
（1）请用含x的式子表示：①销售该图书每本的利润是元，②月销量是件．（用x表示直接写出结果）
（2）若销售图书的月利润为48000元，则每本图书需要售价多少元？
（3）设销售该图书的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？
