Question

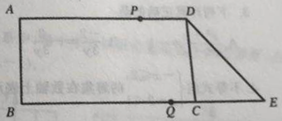
【题目】如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:

(1)求DE的长

(2)当t为多少时,四边形PQED成为平行四边形;

(3)请直接写出使得△DQE是等腰三角形时t的值

Answer 1

【答案】（1）5cm；（2）；（3）t的值为或2或．

【解析】分析:(1)根据平行四边形的性质可得AB∥CD, 利用两直线平行同位角相等可得

∠B=∠DCE=90°,再根据勾股定理即可求出DE,(2)根据一组对边平行且相等的四边形是平行四边形可使PD=QE,即可得9-2t=3t,解得t=.

(3)根据等腰三角形的性质分类讨论, ①以E为圆心ED为半径画圆交BE于一点为点Q,根据ED=EQ,可得5=3t,即可求解, ②以D为圆心ED为半径画圆交BE于一点为点Q,根据等腰三角形性质可得CE=,可得3=t,即可求解,③作线段DE的垂直平分线,可得DQ=EQ,在直角三角形DCQ中,由勾股定理可得:,可得,解方程即可求解.

详解:（1）∵四边形ABCD是平行四边形,

∴AB=CD=4,AB∥CD,

∴∠B=∠DCE=90°,

∴Rt△DCE中,DC=4,CE=3,

∴根据勾股定理,得DE=5cm,

（2）,

根据题意,AP=2t,PD=9-2t,EQ=3t,

∵四边形PQED是平行四边形,

∴PD=QE,

∴9-2t=3t ,

∴t=.

（3）可以使得△DQE是等腰三角形,此时t的值为或2或.